
【题目】现在正是草莓热销的季节,某水果零售商店分两批次从批发市场共购进草莓40箱,已知第一、二次进货价分别为每箱50元、40元,且第二次比第一次多付款700元.
(1)设第一、二次购进草莓的箱数分别为a箱、b箱,求a,b的值;
(2)若商店对这40箱草莓先按每箱60元销售了x箱,其余的按每箱35元全部售完. ①求商店销售完全部草莓所获利润y(元)与x(箱)之间的函数关系式;
②当x的值至少为多少时,商店才不会亏本.
(注:按整箱出售,利润=销售总收入﹣进货总成本)
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2 , 则它移动的距离AA′等于( ) 
A.0.5cm
B.1cm
C.1.5cm
D.2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在桌面上,有6个完全相同的小正方体对成的一个几何体,如图所示.

(1)请画出这个几何体的三视图.
(2)若将此几何A的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有____个.
(3)若另一个几何体B与几何体A的主视图和左视图相同,而小正方体个数则比几何体A多1个,则共有______种添法. 请在图2中画出几何体B的俯视图可能的两种不同情形.
(4)若现在你的手头还有一些相同的小正方体可添放在几何体A上,要保持主视图和左视图不变,则最多可以添___________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条 “折线数轴” .图中点A表示-11,点B表示10,点C表示18,我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.
问:(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、B两点在数轴上相距的长度与Q、O两点在数轴上相距的长度相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图为人民公园中的荷花池,现要测量此荷花池两旁A、B两棵树间的距离(我们不能直接量得).请你根据所学知识,以卷尺和测角仪为测量工具设计一种测量方案.
要求:(1)画出你设计的测量平面图;
(2)简述测量方法,并写出测量的数据(长度用![]() …表示;角度用
…表示;角度用![]() …表示);
…表示);
(3)根据你测量的数据,计算A、B两棵树间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
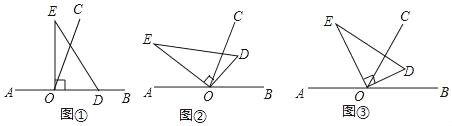
【题目】如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图②,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OC恰好平分∠BOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O转动,如果OD始终在∠BOC的内部,试猜想∠BOD和∠COE有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小丽化简的过程,仔细阅读后解答所提出的问题.
解:a(a+2b)﹣(a﹣1)2﹣2a
=a2+2ab﹣a2﹣2a﹣1﹣2a 第一步
=2ab﹣4a﹣1.第二步
(1)小丽的化简过程从第 步开始出现错误;
(2)请对原整式进行化简,并求当a=![]() ,b=﹣6时原整式的值.
,b=﹣6时原整式的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com