
����Ŀ����ͼ����һ��������ԭ��O�͵�B������һ�£��õ�һ�� ���������ᡱ ��ͼ�е�A��ʾ��11����B��ʾ10����C��ʾ18�����dzƵ�A�͵�C�����������29�����ȵ�λ������P�ӵ�A��������2��λ/����ٶ����š��������ᡱ���������˶����ӵ�O�˶�����B�ڼ��ٶȱ�Ϊԭ����һ�룬֮�����ָ̻�ԭ�٣�ͬʱ������Q�ӵ�C��������1��λ/����ٶ���������ĸ������˶����ӵ�B�˶�����O�ڼ��ٶȱ�Ϊԭ����������֮��Ҳ���ָ̻�ԭ�٣����˶���ʱ��Ϊt�룮
�ʣ���1������P�ӵ�A�˶���C����Ҫ����ʱ�䣿
��2��P��Q��������ʱ�����������M����Ӧ�����Ƕ��٣�
��3����tΪ��ֵʱ��P��B���������������ij�����Q��O���������������ij�����ȣ�

���𰸡���1��19.5���룩����2��M����Ӧ����Ϊ5.��3��t��ֵΪ3��10.5��![]() ��18.
��18.
��������
��1��������߶�AO��OB��BC�ij���,�ֱ����������ʱ,��Ӽ���,
��2������ʱ����ͬ,A��B��·��֮�͵���ȫ��29����λ������ʽ���⼴��,
��3������PB��OQ���,�ɵ÷���,���ݷ��̼������.
��1����P�˶�����Cʱ������ʱ��t =11��2+10��1+8��2=19.5���룩��
��2�������֪��P��Q�����������߶�OB����M������OM=x.
��![]() +x=8+
+x=8+![]() ��
��
x=5 ��
M����Ӧ����Ϊ5.
��3��P��B���������������ij�����Q��O���������������ij��������5�ֿ��ܣ� �ٶ���P��AO�ϣ�����Q��CB�ϣ�����8-t=11-2t,�����t=3.
�ڶ���P��OB�ϣ�����Q��CB�ϣ�����8-t=(t-5.5)![]() ,�����t=6.75,������,��ʱ��P����OB�ϣ�
,�����t=6.75,������,��ʱ��P����OB�ϣ�
�۶���P��OB�ϣ�����Q��BO�ϣ�����(t-5.5)![]() 1=(t-8)
1=(t-8)![]() ,��ã�t=10.5.
,��ã�t=10.5.
�ܶ���P��OB�ϣ�����Q��OA�ϣ�����10-��t-5.5��![]() 1=t-13,�����t=
1=t-13,�����t=![]() ,
,
�ݶ���P��BC�ϣ�����Q��OA�ϣ�����10+2(t-15.5)=t-13+10,�����![]()
���ϣ�t��ֵΪ3��10.5��![]() ��18.
��18.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
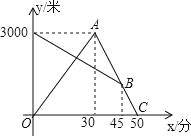
����Ŀ��ij���糿����ǿ�Ӽ��ܲ�ȥ����������ͬʱ��������������������ؼң�;��������������ǿ�ܵ�����������Ҫ���꣬������ԭ·���أ��������������һ��ص��ң���ǿ������ʼ����ͬһ����ֱ�Ĺ�·�����ߣ�����ͼ��������ҵľ���y���ף�����ǿ������ʱ��x���֣�֮��ĺ���ͼ����ͼ����Ϣ����������⣺
��1������ǿ����ʱ���ٶȣ�
��2������Ȱ�ԭ�ٷ�����ǰ���ٷ��ӵ��ң�
��3����ֱ��д����ǿ�������ʱ���1000�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B��������������ͼ��ʾ������OΪԭ�㣬��A��Ӧ��������Ϊa����B��Ӧ��������Ϊb���ҵ�A����ԭ��6����λ���ȣ�a��b����b-|a|=2��
(1)a=______��b=______��
(2)����P�ӵ�A��������ÿ��2����λ���ȵ��ٶ������˶������˶�ʱ��Ϊt�루t��0��
�ٵ�PO=2PBʱ�����P���˶�ʱ��t��
�ڵ�PB=6ʱ����t��ֵ��
(3)����P�˶����߶�OB��ʱ���ֱ�ȡAP��OB���е�E��F����![]() ��ֵ�Ƿ�Ϊһ����ֵ������ǣ������ֵ��������ǣ�˵�����ɣ�
��ֵ�Ƿ�Ϊһ����ֵ������ǣ������ֵ��������ǣ�˵�����ɣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��C Ϊ�߶� AD ��һ����B Ϊ CD ���е���AD=13cm��BD=3cm��
��1��ͼ�й��� ���߶Σ�
��2���� AC �ij���
��3������ E ���߶� AD �ϣ��� BE=2cm���� AE �ij���
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�߳�Ϊm�����������Ϊ12�������й���m��˵���У�������ǣ� ��
��m������������m�Ƿ���m2 -12=0�Ľ⣻��m���㲻��ʽ��![]() ����m��12������ƽ������
����m��12������ƽ������
A. �٢� B. �٢� C. �� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Dz�ݮ�����ļ��ڣ�ijˮ�������̵�������δ������г���������ݮ40�䣬��֪��һ�����ν����۷ֱ�Ϊÿ��50Ԫ��40Ԫ���ҵڶ��αȵ�һ�ζึ��700Ԫ��
��1�����һ�����ι�����ݮ�������ֱ�Ϊa�䡢b�䣬��a��b��ֵ��
��2�����̵����40���ݮ�Ȱ�ÿ��60Ԫ������x�䣬����İ�ÿ��35Ԫȫ�����꣮ �����̵�������ȫ����ݮ��������y��Ԫ����x���䣩֮��ĺ�����ϵʽ��
�ڵ�x��ֵ����Ϊ����ʱ���̵�Ų��������
��ע����������ۣ�����=���������멁�����ܳɱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ABΪֱ���ġ�O�ֱ���BC��AC�ཻ�ڵ�D��E��BD=CD������D����O�����߽���AC�ڵ�F�� 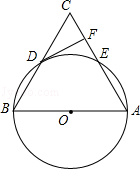
��1����֤��DF��AC��
��2������O�İ뾶Ϊ5����CDF=30�㣬�� ![]() �ij�����������У���
�ij��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��չ�ˡ�����ϲ������ʦ����ѡ���ȷ��������ѡ��������ѧ���ͽ�ʦ������4����ѡ��ʦ����ͶƱ��ÿƱѡ1����ѡ��ʦ��ÿλ��ѡ��ʦ�õ��Ľ�ʦƱ����5����ѧ��Ʊ���ĺ���Ϊ�ý�ʦ����Ʊ���������Ǹ���ѧ���ͽ�ʦ����ͶƱ������Ƶ�ͳ�Ʊ�������ͳ��ͼ������������ ѧ��ͶƱ���ͳ�Ʊ�
��ѡ��ʦ | ����ʦ | ����ʦ | ����ʦ | ����ʦ |
��Ʊ�� | 200 | 300 |
��1��������25λ��ʦ�����μ�ͶƱ��������ʦ�õ��Ľ�ʦƱ���Ƕ��٣��벹ȫ����ͳ��ͼ�������ڴ𰸾����Ӧ��ͼ�ϣ�
��2������ʦ������ʦ�õ���ѧ����Ʊ����600���Ҷ���ʦ�õ���ѧ��Ʊ��������ʦ�õ���ѧ��Ʊ����3����40Ʊ������ʦ������ʦ�õ���ѧ��Ʊ���ֱ��Ƕ��٣�
��3���ڣ�1������2���������£����ܵ�Ʊ���ϸߵ�2����ʦ��ѡ���в���������Ϊ��ѡ�����������λ��ʦ��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB=130��������OC����AOB�ڲ�����һ�����ߣ�OD��OE�ֱ�����AOC����BOC�Ľ�ƽ���ߣ�����������ȷ���ǣ�������
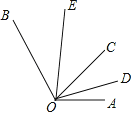
A. ��DOE�Ķ�������ȷ�� B. ��AOD=![]() ��EOC
��EOC
C. ��AOD+��BOE=65�� D. ��BOE=2��COD
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com