
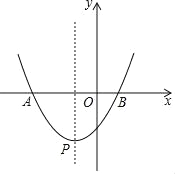
【题目】二次函数![]() 的图象如图所示,则下列结论中:①
的图象如图所示,则下列结论中:①![]()
![]()
![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤当
;⑤当![]() 时,
时,![]() 随
随![]() 的增大而增大.以上结论正确的有________(只填序号)
的增大而增大.以上结论正确的有________(只填序号)
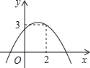
【答案】①②④
【解析】
①根据二次函数开口向下可判断a的正负,由对称轴大于0可判断b的正负,由于二次函数交于y轴正半轴可判断c的正负;
②令x=2,根据图象即可得出答案;
③对称轴为直线x=-![]() ,根据图象即可得出答案;
,根据图象即可得出答案;
④二次函数y=ax2+bx+c与x轴有两个交点,即可得△>0;
⑤由图象可知当x<2时,y随x的增大先增大后减小.
①根据二次函数开口向下,∴a<0,对称轴为x=![]() >0,∴b>0,二次函数交于y轴正半轴,∴c>0,故本小题正确;
>0,∴b>0,二次函数交于y轴正半轴,∴c>0,故本小题正确;
②令x=2,由图象知:y=4a+2b+c=3,故本小题正确;
③对称轴为直线x=![]() ,由图象知:
,由图象知:![]() <2,故本小题错误;
<2,故本小题错误;
④∵二次函数y=ax2+bx+c与x轴有两个交点,即可得△>0,∴b24ac>0,故本小题正确;
⑤由图象可知当x<2时,y随x的增大先增大后减小,故本小题错误;
故正确的有①②④。
故答案为:①②④。


科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的实验时,绘出的某一结果出现的频率折线图,则符合这一结果的实验可能是( )

A. 抛一枚硬币,出现正面朝上
B. 掷一个正六面体的骰子,出现3点朝上
C. 一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D. 从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象经过点(-2,0),(x0,0),1<x0<2,与y轴的负半轴相交,且交点在(0,-2)的上方,下列结论:
①b>0;②2a<b;③2a-b-1<0;④2a+c<0.其中正确结论是 _________(填正确序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=2x2-4x-6与x轴交于点A、B,与y轴交于点C.有下列说法:①抛物线的对称轴是x=1;②A、B两点之间的距离是4;③△ABC的面积是24;④当x<0时,y随x的增大而减小.其中,说法正确的是_________________.(只需填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两棵树的高度分别为AB=6 m,CD=8 m,两树的根部间的距离AC=4 m,小强沿着正对这两棵树的方向从左向右前进,如果小强的眼睛与地面的距离为1.6 m,当小强与树AB的距离小于多少时,就不能看到树CD的树顶D?
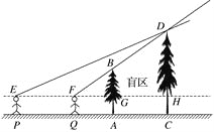
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]() ,下列说法错误的是( )
,下列说法错误的是( )
A. 当![]() 时,
时,![]() 随
随![]() 的增大而减小
的增大而减小
B. 若图象与![]() 轴有交点,则
轴有交点,则![]()
C. 当![]() 时,不等式
时,不等式![]() 的解集是
的解集是![]()
D. 若将图象向上平移![]() 个单位,再向左平移
个单位,再向左平移![]() 个单位后过点
个单位后过点![]() ,则
,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
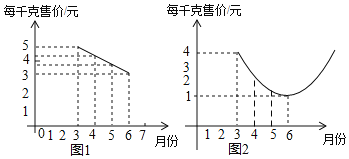
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?简单说明理由.
(3)已知市场部销售该种蔬菜4、5两个月的总收益为22万元,且5月份的销售量比4月份的销售量多2万千克,求4、5两个月的销售量分别是多少万千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
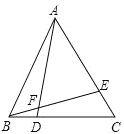
【题目】如图,△ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F,
(1)证明:△ABD≌△BCE;
(2)证明:△ABE∽△FAE;
(3)若AF=7,DF=1,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴相交于点A(﹣3,0),B(1,0),与y轴相交于(0,﹣![]() ),顶点为P.
),顶点为P.
(1)求抛物线解析式;
(2)在抛物线是否存在点E,使△ABP的面积等于△ABE的面积?若存在,求出符合条件的点E的坐标;若不存在,请说明理由;
(3)坐标平面内是否存在点F,使得以A、B、P、F为顶点的四边形为平行四边形?直接写出所有符合条件的点F的坐标,并求出平行四边形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com