
【题目】抛物线y=2x2-4x-6与x轴交于点A、B,与y轴交于点C.有下列说法:①抛物线的对称轴是x=1;②A、B两点之间的距离是4;③△ABC的面积是24;④当x<0时,y随x的增大而减小.其中,说法正确的是_________________.(只需填写序号)
【答案】①②④
【解析】
根据二次函数的对称轴公式得出抛物线的对称轴,即可判断①;解方程2x2-4x-6=0求出点A、B的横坐标,即可判断②;求出AB的长及点C的坐标,得出△ABC的面积,即可判断③;根据二次函数的增减性即可判断④.
解:①抛物线y=2x2-4x-6的对称轴是直线x=-![]() =1,故①正确;
=1,故①正确;
②2x2-4x-6=0,解得x=-1或3,所以AB=4;故②正确;
③∵AB=4,C(0,-6),
∴S△ABC=![]() ×4×6=12,故③错误;
×4×6=12,故③错误;
④∵抛物线y=2x2-4x-6的开口向上,对称轴是直线x=1,
∴当x<1时,y随x的增大而减小;x>1时,y随x的增大而增大;
∴当x<0时,y随x的增大而减小,故④正确,
所以正确的是①②④.
故答案为:①②④.


科目:初中数学 来源: 题型:
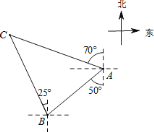
【题目】如图,轮船在![]() 处观测灯塔
处观测灯塔![]() 位于北偏西
位于北偏西![]() 方向上,轮船从
方向上,轮船从![]() 处以每小时
处以每小时![]() 海里的速度沿南偏西
海里的速度沿南偏西![]() 方向匀速航行,
方向匀速航行,![]() 小时后到达码头
小时后到达码头![]() 处,此时,观测灯塔
处,此时,观测灯塔![]() 位于北偏西
位于北偏西![]() 方向上,则灯塔
方向上,则灯塔![]() 与码头
与码头![]() 的距离是____海里.(结果精确到个位,参考数据:
的距离是____海里.(结果精确到个位,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
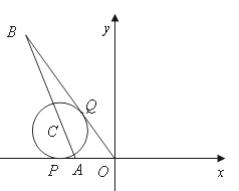
【题目】如图,直线y=-2x-10与x轴交于点A,直线y=-![]() x交于点B,点C在线段AB上,⊙C与x轴相切于点P,与OB切于点Q.求:(1)A点的坐标;(2)OB的长;(3)C点的坐标.
x交于点B,点C在线段AB上,⊙C与x轴相切于点P,与OB切于点Q.求:(1)A点的坐标;(2)OB的长;(3)C点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
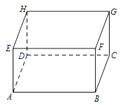
【题目】如图 所示,一个长方体的长、宽、高分别是 ![]() ,
,![]() ,
,![]() ,有一只蚂蚁从点
,有一只蚂蚁从点 ![]() 出发沿棱爬行,每条棱不允许重复,则蚂蚁回到点
出发沿棱爬行,每条棱不允许重复,则蚂蚁回到点 ![]() 时,最多爬行多远?并把蚂蚁所爬行的路线用字母按顺序表示出来.
时,最多爬行多远?并把蚂蚁所爬行的路线用字母按顺序表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
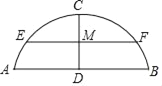
【题目】如图是一座跨河拱桥,桥拱是圆弧形,跨度AB为16米,拱高CD为4米.
(1)求桥拱的半径R.
(2)若大雨过后,桥下水面上升到EF的位置,且EF的宽度为12米,求拱顶C到水面EF的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
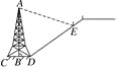
【题目】如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=24 m,小明和小华的身高都是1.6 m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2 m和1 m,那么塔高AB为________ m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图,点P是y=
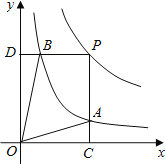
在第一象限内的图象如图,点P是y=![]() 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y=![]() 的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=
的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=![]() AP.其中所有正确结论的序号是( )
AP.其中所有正确结论的序号是( )
A. ①②③ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某购物中心试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价且获利不得高于 50%.经试销发现,销售量y(件)与销售单价x(元)的关系符合一次函数yx140.
(1)若销售该服装获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价为多少元时,可获得最大利润?最大利润是多少元?
(2)当获得利润为1200元时,求销售单价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com