
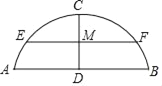
【题目】如图是一座跨河拱桥,桥拱是圆弧形,跨度AB为16米,拱高CD为4米.
(1)求桥拱的半径R.
(2)若大雨过后,桥下水面上升到EF的位置,且EF的宽度为12米,求拱顶C到水面EF的高度.
科目:初中数学 来源: 题型:
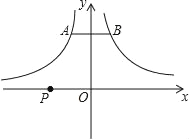
【题目】如图,点A(m,2),B(n,2)分别是反比例函数y=﹣![]() ,y=
,y=![]() 在x轴上方的图象上的点,点P是x轴上的动点,则PA+PB的最小值为_____.
在x轴上方的图象上的点,点P是x轴上的动点,则PA+PB的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
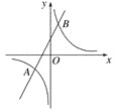
【题目】如图,直线y=2x+4与反比例函数y=![]() 的图象相交于A(-3,a)和B两点.
的图象相交于A(-3,a)和B两点.
(1)求k的值;
(2)直线y=m(m>0)与直线AB相交于点M,与反比例函数的图象相交于点N.若MN=4,求m的值;
(3)直接写出不等式![]() >x的解集.
>x的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象经过点(-2,0),(x0,0),1<x0<2,与y轴的负半轴相交,且交点在(0,-2)的上方,下列结论:
①b>0;②2a<b;③2a-b-1<0;④2a+c<0.其中正确结论是 _________(填正确序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张正方形纸片的4个角剪去4个大小一样的小正方形,然后折起来就可以制成一个无盖的长方体纸盒,设这个正方形纸片的边长为a,这个无盖的长方体盒子高为h.
(1)若a=18cm,h=4cm,则这个无盖长方体盒子的底面面积为 ;
(2)用含a和h的代数式表示这个无盖长方体盒子的容积V= ;
(3)若a=18cm,试探究:当h越大,无盖长方体盒子的容积V就越大吗?请举例说明;这个无盖长方体盒子的最大容积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=2x2-4x-6与x轴交于点A、B,与y轴交于点C.有下列说法:①抛物线的对称轴是x=1;②A、B两点之间的距离是4;③△ABC的面积是24;④当x<0时,y随x的增大而减小.其中,说法正确的是_________________.(只需填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
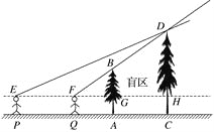
【题目】如图,两棵树的高度分别为AB=6 m,CD=8 m,两树的根部间的距离AC=4 m,小强沿着正对这两棵树的方向从左向右前进,如果小强的眼睛与地面的距离为1.6 m,当小强与树AB的距离小于多少时,就不能看到树CD的树顶D?
查看答案和解析>>
科目:初中数学 来源: 题型:
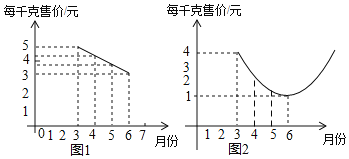
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?简单说明理由.
(3)已知市场部销售该种蔬菜4、5两个月的总收益为22万元,且5月份的销售量比4月份的销售量多2万千克,求4、5两个月的销售量分别是多少万千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
(1)求抛物线的解析式;
(2)抛物线上是否存在点M,使得⊿CDM是以CD为直角边的直角三角形?若存在,请求出M点的坐标;若不存在,请说明理由.
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,,连接QE.若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由。


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com