
【题目】有这样的题目:把方程![]() x2-x=2化为一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.现在把上面的题目改编成下面的两个小题,请回答问题:
x2-x=2化为一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.现在把上面的题目改编成下面的两个小题,请回答问题:
(1)下面式子中是方程![]() x2-x=2化为一元二次方程的一般形式的是________.(只填写序号)
x2-x=2化为一元二次方程的一般形式的是________.(只填写序号)
①![]() x2-x-2=0,②-
x2-x-2=0,②- ![]() x2+x+2=0,③x2-2x=4,④-x2+2x+4=0,⑤
x2+x+2=0,③x2-2x=4,④-x2+2x+4=0,⑤![]() x2-2
x2-2![]() x-4
x-4![]() =0.
=0.
(2)方程![]() x2-x=2化为一元二次方程的一般形式后,它的二次项系数,一次项系数和常数项之间具有什么关系?
x2-x=2化为一元二次方程的一般形式后,它的二次项系数,一次项系数和常数项之间具有什么关系?
【答案】(1) ①②④⑤;(2)见解析
【解析】试题分析:(1)把方程通过移项或根据等式的性质两边同乘以-1,-2,2![]() 即可变形得到正确选项;
即可变形得到正确选项;
(2)通过观察可找到的二次项系数,一次项系数,常数项之间具有的关系是,二次项系数:一次项系数:常数项=1:(-2):(-4).
试题解析:(1)![]() x2-x=2,移项得:
x2-x=2,移项得: ![]() x2-x-2=0,所以①是一般形式,①两边同乘-1,得:-
x2-x-2=0,所以①是一般形式,①两边同乘-1,得:-![]() x2+x+2=0,故②是一般形式,③不是一般形式,①两边同乘-2得:-x2+2x+4=0,故④是一般形式,①两边同乘2
x2+x+2=0,故②是一般形式,③不是一般形式,①两边同乘-2得:-x2+2x+4=0,故④是一般形式,①两边同乘2![]() 得:
得: ![]() x2-2
x2-2![]() x-4
x-4![]() =0,故⑤是一般形式,
=0,故⑤是一般形式,
故答案为:①②④⑤;
(2) 若设它的二次项系数为a(a≠0),则一次项系数为-2a,常数项为-4a.(即满足二次系数∶一次项系数∶常数项=1∶-2∶-4).


科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有2个白球和1个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球(不放回),再从余下的2个球中任意摸出1个球.
(1)用树状图或列表等方法列出所有可能出现的结果;
(2)求两次摸到的球的颜色不同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知任意三角形ABC,过点C作DE∥AB;
①求证:∠DCA=∠A; ②求证:∠A+∠B+∠ACB=180°;
(2)如图(2),求证:∠AGF=∠AEF+∠F;
(3)如图(3),AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=150°,求∠F.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中每个小正方形边长为1,△ABC的顶点都在格点上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)画出平移后的△A′B′C′的中线B′D′
(3)若连接BB′,CC′,则这两条线段的关系是________
(4)△ABC在整个平移过程中线段AB 扫过的面积为________
(5)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有______个
(注:格点指网格线的交点)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如下表:
甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
且![]() =8,
=8, ![]() =1.8.根据上述信息完成下列问题:
=1.8.根据上述信息完成下列问题:
(1)将甲运动员的折线统计图补充完整.
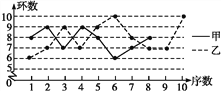
(2)求乙运动员射击训练成绩的众数和中位数.
(3)求甲运动员射击成绩的平均数和方差,并判断甲、乙两人本次射击成绩的稳定性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)-23+![]() (2 018+3)0-
(2 018+3)0-![]() ; (2)992-69×71;
; (2)992-69×71;
(3) ![]() ÷(-3xy); (4)(-2+x)(-2-x);
÷(-3xy); (4)(-2+x)(-2-x);
(5)(a+b-c)(a-b+c); (6)(3x-2y+1)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )

A. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B. 一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C. 暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D. 掷一个质地均匀的正六面体骰子,向上的面点数是4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=mx2-(m+5)x+5.
(1)求证:它的图象与x轴必有交点,且过x轴上一定点;
(2)这条抛物线与x轴交于两点A(x1,0),B(x2,0),且0<x1<x2,过(1) 中定点的直线L;y=x+k交y轴于点D,且AB=4,圆心在直线L上的⊙M为A、B两点,求抛物线和直线的关系式,弦AB与弧![]() 围成的弓形面积.
围成的弓形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
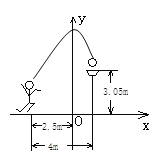
【题目】如图所示,一位篮球运动员在离篮圈水平距离为4m处跳起投篮,球沿一条抛物线运行,当球运行的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心离地面距离为3.05m.
(1)建立如图所示的直角坐标系,求抛物线所对应的函数关系式;
(2)若该运动员身高1.8m,这次跳投时,球在他头顶上方0.25m处出手.问:球出手时,他跳离地面多高?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com