
【题目】计算:
(1)-23+![]() (2 018+3)0-
(2 018+3)0-![]() ; (2)992-69×71;
; (2)992-69×71;
(3) ![]() ÷(-3xy); (4)(-2+x)(-2-x);
÷(-3xy); (4)(-2+x)(-2-x);
(5)(a+b-c)(a-b+c); (6)(3x-2y+1)2.
【答案】(1)原式=-16![]() ;(2)原式=4 902;(3)原式=-
;(2)原式=4 902;(3)原式=-![]() x2y2-
x2y2-![]() xy+1;(4)原式=4-x2;(5)原式=a2-b2-c2+2bc;(6)原式=9x2+4y2-12xy+6x-4y+1.
xy+1;(4)原式=4-x2;(5)原式=a2-b2-c2+2bc;(6)原式=9x2+4y2-12xy+6x-4y+1.
【解析】试题分析:(1)第一项表示23的相反数,第二项非零数的零次幂等于1,第三项负整数指数幂等于这个数正整数指数幂的倒数;(2)把69×71改写成(70-1)×(70+1)计算;(3)按照多项式除以单项式的法则计算;(4)利用平方差公式计算;(5)把原式改写成[a+(b+c)][ a-(b+c)], 先根据平方差公式计算,再用完全平方公式计算;(6)把原式改写成[(3x-2y)+1]2,根据完全平方公式计算.
解:(1)原式=-8+![]() -9=-17+
-9=-17+![]() =-16
=-16![]() .
.
(2)原式=(100-1)2-(70-1)×(70+1)=10 000-200+1-4 900+1=4 902.
(3)原式=-![]() x2y2-
x2y2-![]() xy+1.
xy+1.
(4)原式=(-2)2-x2=4-x2.
(5)原式=a2-![]() =a2-b2-c2+2bc.
=a2-b2-c2+2bc.
(6)原式=[(3x-2y)+1]2
=(3x-2y)2+2(3x-2y)+1
=9x2+4y2-12xy+6x-4y+1.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】下列调查中,适宜采用全面调查方式的是( )
A.调查热播电视剧《人民的名义》的收视率
B.调查广州市民对皮影表演艺术的喜爱程度
C.调查某班学生对社会主义核心价值观的知晓率
D.调查我国首艘货运飞船“天舟一号”的零部件质量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小丽在操场上玩耍,小丽突然高兴地对小明说:“我踩到你的‘脑袋’了.”如图即表示此时小明和小丽的位置.

(1)请画出此时小丽在阳光下的影子;
(2)若已知小明的身高为1.60 m,小明和小丽之间的距离为2 m,而小丽的影子长为1.75 m,求小丽的身高.
查看答案和解析>>
科目:初中数学 来源: 题型:
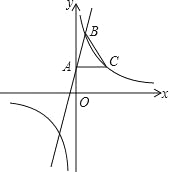
【题目】如图,在平面直角坐标系xOy中,一次函数y=3x+2的图象与y轴交于点A,与反比例函数y=![]() (k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=
(k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=![]() (k≠0)的图象于点C,连接BC.
(k≠0)的图象于点C,连接BC.
(1)求反比例函数的表达式.
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样的题目:把方程![]() x2-x=2化为一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.现在把上面的题目改编成下面的两个小题,请回答问题:
x2-x=2化为一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.现在把上面的题目改编成下面的两个小题,请回答问题:
(1)下面式子中是方程![]() x2-x=2化为一元二次方程的一般形式的是________.(只填写序号)
x2-x=2化为一元二次方程的一般形式的是________.(只填写序号)
①![]() x2-x-2=0,②-
x2-x-2=0,②- ![]() x2+x+2=0,③x2-2x=4,④-x2+2x+4=0,⑤
x2+x+2=0,③x2-2x=4,④-x2+2x+4=0,⑤![]() x2-2
x2-2![]() x-4
x-4![]() =0.
=0.
(2)方程![]() x2-x=2化为一元二次方程的一般形式后,它的二次项系数,一次项系数和常数项之间具有什么关系?
x2-x=2化为一元二次方程的一般形式后,它的二次项系数,一次项系数和常数项之间具有什么关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
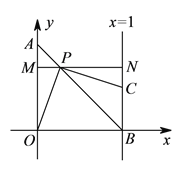
【题目】如图,以![]() 为原点的直角坐标系中,
为原点的直角坐标系中,![]() 点的坐标为
点的坐标为![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .点
.点![]() 为线段
为线段![]() 上一动点,作直线
上一动点,作直线![]() ,交直线
,交直线![]() 于点
于点![]() .过
.过![]() 点作直线
点作直线![]() 平行于
平行于![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .记
.记![]() ,
,![]() 的面积为
的面积为![]() .
.
(![]() )当点
)当点![]() 在第一象限时:求证:
在第一象限时:求证:![]() ≌
≌![]() .
.
(![]() )当点
)当点![]() 在线段
在线段![]() 上移动时,点
上移动时,点![]() 也随之在直线
也随之在直线![]() 上移动,求出
上移动,求出![]() 与
与![]() 之间的函数关系式,并写出自变量的取值范围.
之间的函数关系式,并写出自变量的取值范围.
(![]() )当点
)当点![]() 在线段
在线段![]() 上移动时,
上移动时,![]() 是否可能成为等腰三角形?如果可能,直接写出所有能使
是否可能成为等腰三角形?如果可能,直接写出所有能使![]() 成为等腰三角形的
成为等腰三角形的![]() 的值;如果不可能,请说明理由.
的值;如果不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
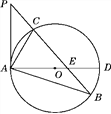
【题目】如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG·AB=12,求AC的长;(3)在满足(2)的条件下,若AF∶FD=1∶2,GF=1,求⊙O的半径及sin∠ACE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠BCF=∠B+∠F.求证:AB//EF .
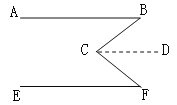
证明:经过点C作CD//AB
∴∠BCD=∠B.( )
∵∠BCF=∠B+∠F,(已知)
∴∠ ( )=∠F.( )
∴CD//EF.( )
∴AB//EF( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com