
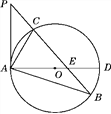
【题目】如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG·AB=12,求AC的长;(3)在满足(2)的条件下,若AF∶FD=1∶2,GF=1,求⊙O的半径及sin∠ACE的值.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】分析:(1)根据圆周角定理得出∠ACD=90°以及利用∠PAC=∠PBA得出∠CAD+∠PAC=90°进而得出答案;
(2)首先得出△CAG∽△BAC,进而得出![]() ,求出AC即可;
,求出AC即可;
(3)先求出AF的长,根据勾股定理得:![]() ,即可得出sin∠ADB=
,即可得出sin∠ADB=![]() ,利用∠ACE=∠ACB=∠ADB,求出即可.
,利用∠ACE=∠ACB=∠ADB,求出即可.
本题解析:(1)证明:连接CD,
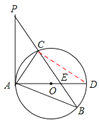

∵AD是⊙O的直径,∴∠ACD=90° ∴∠CAD+∠ADC=90°。
又∵∠PAC=∠PBA,∠ADC=∠PBA, ∴∠PAC=∠ADC。∴∠CAD+∠PAC=90° ∴PA⊥OA。
又∵AD是⊙O的直径,∴PA是⊙O的切线。
(2)由(1)知,PA⊥AD,又∵CF⊥AD,∴CF∥PA。∴∠GCA=∠PAC。
又∵∠PAC=∠PBA,∴∠GCA=∠PBA。
又∵∠CAG=∠BAC,∴△CAG∽△BAC。 ∴![]() ,即AC2=AGAB。
,即AC2=AGAB。
∵AGAB=12,∴AC2=48。∴AC=![]() 。
。
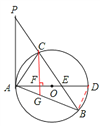
(3)设AF=x, ∵AF:FD=1:2,∴FD=2x。∴AD=AF+FD=3x。
在Rt△ACD中,∵CF⊥AD,∴AC2=AFAD,即3x2=48。
解得;x=4。 ∴AF=4,AD=12。∴⊙O半径为6。
在Rt△AFG中,∵AF=4,GF=2,
∴根据勾股定理得:![]()
由(2)知,AGAB=48 ![]()
连接BD,∵AD是⊙O的直径,∴∠ABD=90°。
在Rt△ABD中,∵sin∠ADB=![]() ,AD=12,
,AD=12,![]() ∴sin∠ADB=
∴sin∠ADB=![]() 。
。
∵∠ACE=∠ACB=∠ADB,∴sin∠ACE=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)-23+![]() (2 018+3)0-
(2 018+3)0-![]() ; (2)992-69×71;
; (2)992-69×71;
(3) ![]() ÷(-3xy); (4)(-2+x)(-2-x);
÷(-3xy); (4)(-2+x)(-2-x);
(5)(a+b-c)(a-b+c); (6)(3x-2y+1)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师家买了一套新房,其结构如图所示(单位:m).他打算将卧室铺上木地板,其余部分铺上地砖.
(1)木地板和地砖分别需要多少平方米?
(2)如果地砖的价格为每平方米x元,木地板的价格为每平方米3x元,那么王老师需要花多少钱?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=mx2-(m+5)x+5.
(1)求证:它的图象与x轴必有交点,且过x轴上一定点;
(2)这条抛物线与x轴交于两点A(x1,0),B(x2,0),且0<x1<x2,过(1) 中定点的直线L;y=x+k交y轴于点D,且AB=4,圆心在直线L上的⊙M为A、B两点,求抛物线和直线的关系式,弦AB与弧![]() 围成的弓形面积.
围成的弓形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,∠B <∠C,AD,AE分别是△ABC的高和角平分线。
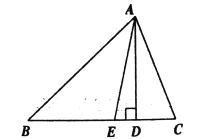
(1)若∠B=30°,∠C=50°,试确定∠DAE的度数;
(2)试写出∠DAE,∠B,∠C的数量关系,并证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
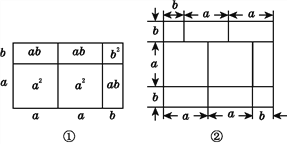
【题目】先阅读再解答:我们已经知道,根据几何图形的面积关系可以说明完全平方公式,实际上还有一些等式也可以用这种方式加以说明,例如:
(2a+b)(a+b)=2a2+3ab+b2,就可以用图①的面积关系来说明.
(1)根据图②写出一个等式: ;
(2)已知等式:(x+p)(x+q)=x2+(p+q)x+pq,请你画出一个相应的几何图形加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线L;y=ax2+bx+c(其中a、b、c都不等于0), 它的顶点P的坐标是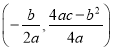 ,与y轴的交点是M(0,c)我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.
,与y轴的交点是M(0,c)我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.
(1)请直接写出抛物线y=2x2-4x+1的伴随抛物线和伴随直线的关系式:
伴随抛物线的关系式_________________
伴随直线的关系式___________________
(2)若一条抛物线的伴随抛物线和伴随直线分别是y=-x2-3和y=-x-3, 则这条抛物线的关系是___________:
(3)求抛物线L:y=ax2+bx+c(其中a、b、c都不等于0) 的伴随抛物线和伴随直线的关系式;
(4)若抛物线L与x轴交于A(x1,0),B(x2,0)两点x2>x1>0,它的伴随抛物线与x 轴交于C,D两点,且AB=CD,请求出a、b、c应满足的条件.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com