
【题目】已知抛物线y=mx2-(m+5)x+5.
(1)求证:它的图象与x轴必有交点,且过x轴上一定点;
(2)这条抛物线与x轴交于两点A(x1,0),B(x2,0),且0<x1<x2,过(1) 中定点的直线L;y=x+k交y轴于点D,且AB=4,圆心在直线L上的⊙M为A、B两点,求抛物线和直线的关系式,弦AB与弧![]() 围成的弓形面积.
围成的弓形面积.
【答案】(1)证明见解析;(2)![]()
【解析】本题主要考查了二次函数与一元二次方程的联系、根的判别式、函数图象与坐标轴交点坐标的求法、函数解析式的确定、扇形面积的计算方法等
(1)若抛物线于x轴有交点,那么当y=0时,所得方程的根的判别式恒大于等于0,可据此进行证明;将抛物线解析式的右边,用十字相乘法进行因式分解,可得:y=(mx-5)(x-1),由此可看出抛物线一定经过点(1,0).
(2)由于抛物线交x轴于A、B两点,且A在B左侧,且A、B都在原点的右侧,因此A(1,0),B(5,0),根据A点坐标,可确定直线的解析式,根据A、B的坐标,可确定抛物线的解析式;
若⊙M同时经过A、B两点,根据抛物线和圆的对称性知:点M必为抛物线对称轴与直线的交点,由此可求得点M的坐标为(3,2),而AB=4,因此△ABM是个等腰直角三角形,即可得到![]() 的圆心角,那么扇形MAB的面积减去等腰直角三角形MAB的面积即为所求弓形的面积.
的圆心角,那么扇形MAB的面积减去等腰直角三角形MAB的面积即为所求弓形的面积.
(1)证明:∵y=mx2-(m+5)x+5,∴△=[-(m+5)]2-4m×5=m2+10m+25-20m="(m-" 5)2.
不论m取任何实数,(m-5)2≥0,即△≥0,故抛物线与x轴必有交点.
又∵x轴上点的纵坐标均为零,∴令y=0,代入y=mx2-(m+5)x+5,得
mx2-(m+5)x+ 5=0,(mx-5)(x-1)=0,
∴x=![]() 或x=1.故抛物线必过x轴上定点(1,0).
或x=1.故抛物线必过x轴上定点(1,0).
(2)解:如答图所示,
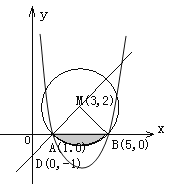
∵L:y=x+k,把(1,0)代入上式,
得0=1+k,∴k=-1,∴y="x-1."
又∵抛物线与x轴交于两点A(x1,0),B(x2,0),且0<x1<x2,AB=4,
∵x1x2>0,∴x1="1," x2=5,∴A(1,0),B(5,0),
把B(5,0)代入y=mx2-(m+5)x+5,得0=25m-(m+5)×5+5.
∴m=1,∴y=x2-6x+5.
∵M点既在直线L:y=x-1上,又在线段AB的垂直平分线上,
∴M点的横坐标x1+![]() =1+
=1+![]() .
.
把x=3代入y=x-1,得y=2.
∴圆心M(3,2),∴半径r=MA=MB=![]() ,
,
∴MA2=MB2=8.
又AB2=42= 16,∴MA2+MB2=AB2,
∴△ABM为直角三角形,且∠AMB=90°,
∴S弓形ACB=S扇形AMB- S△ABM=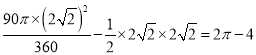 .
.


科目:初中数学 来源: 题型:
【题目】有这样的题目:把方程![]() x2-x=2化为一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.现在把上面的题目改编成下面的两个小题,请回答问题:
x2-x=2化为一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.现在把上面的题目改编成下面的两个小题,请回答问题:
(1)下面式子中是方程![]() x2-x=2化为一元二次方程的一般形式的是________.(只填写序号)
x2-x=2化为一元二次方程的一般形式的是________.(只填写序号)
①![]() x2-x-2=0,②-
x2-x-2=0,②- ![]() x2+x+2=0,③x2-2x=4,④-x2+2x+4=0,⑤
x2+x+2=0,③x2-2x=4,④-x2+2x+4=0,⑤![]() x2-2
x2-2![]() x-4
x-4![]() =0.
=0.
(2)方程![]() x2-x=2化为一元二次方程的一般形式后,它的二次项系数,一次项系数和常数项之间具有什么关系?
x2-x=2化为一元二次方程的一般形式后,它的二次项系数,一次项系数和常数项之间具有什么关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,AB是⊙O的直径,且AB=10,C是⊙O上的动点,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D.(1)求证:∠DAC=∠BAC;
(2)若AD和⊙O相切于点A,求AD的长;
(3)若把直线EF向上平行移动,如图②,EF交⊙O于G,C两点,题中的其他条件不变,试问这时与∠DAC相等的角是否存在,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
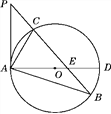
【题目】如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG·AB=12,求AC的长;(3)在满足(2)的条件下,若AF∶FD=1∶2,GF=1,求⊙O的半径及sin∠ACE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
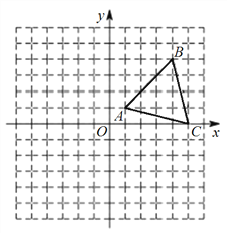
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)写出点B的坐标为________;
(2)将△ABC向左平移5个单位长度,再向下平移3个单位长度,画出平移后得到的△A1B1C1,并直接写出点A1的坐标为________;点C1的坐标为________;
(3)△A1B1C1的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b(k≠0)与两坐标轴分别交于点B,C,点A的坐标为(-2,0)点D的坐标为(1,0)
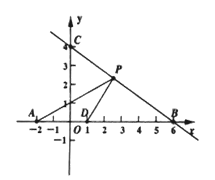
(1)试确定直线BC的函数关系式.
(2)若p(x,y)是直线BC在第一象限内的一个动点,试写出△ADP的面积S与x的函数关系式.
(3)当P运动到什么位置时,△ADP的面积为3?请写出此时点P的坐标,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
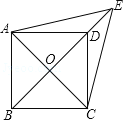
【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com