
【题目】如图,直线y=kx+b(k≠0)与两坐标轴分别交于点B,C,点A的坐标为(-2,0)点D的坐标为(1,0)
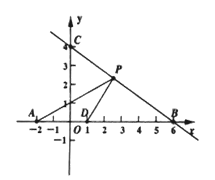
(1)试确定直线BC的函数关系式.
(2)若p(x,y)是直线BC在第一象限内的一个动点,试写出△ADP的面积S与x的函数关系式.
(3)当P运动到什么位置时,△ADP的面积为3?请写出此时点P的坐标,并说明理由.
【答案】(1)y=-![]() x+4;(2) S=-x+6;(3) (3,2)
x+4;(2) S=-x+6;(3) (3,2)
【解析】(1)运用待定系数法即可求出解析式;
(2)利用三角形面积公式即可建立函数关系式;
(3)利用(2)中的函数关系式即可得出答案.
解:(1)设直线BC的函数关系式为y=kx+b(k≠0),
由题意,得方程组,![]() ,
,
解得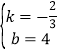 ,
,
所以,函数y与x的函数关系式为y=-![]() x+4;
x+4;
(2)由题意,P(x,y)是直线BC在第一象限的点,
∴y>0,且y=-![]() x+4,
x+4,
又,点A的坐标为(-2,0),点D的坐标为(1,0),
∴AD=3,
∴S△ADP=![]() ×3×〔-
×3×〔-![]() x+4 〕=-x+6,
x+4 〕=-x+6,
即S=-x+6;
(3)当S=3时,
-x+6=3,
解得x=3,
所以y=-![]() ×3+4=2,
×3+4=2,
此时,点P的坐标为(3,2).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,网格中每个小正方形边长为1,△ABC的顶点都在格点上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)画出平移后的△A′B′C′的中线B′D′
(3)若连接BB′,CC′,则这两条线段的关系是________
(4)△ABC在整个平移过程中线段AB 扫过的面积为________
(5)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有______个
(注:格点指网格线的交点)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=mx2-(m+5)x+5.
(1)求证:它的图象与x轴必有交点,且过x轴上一定点;
(2)这条抛物线与x轴交于两点A(x1,0),B(x2,0),且0<x1<x2,过(1) 中定点的直线L;y=x+k交y轴于点D,且AB=4,圆心在直线L上的⊙M为A、B两点,求抛物线和直线的关系式,弦AB与弧![]() 围成的弓形面积.
围成的弓形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读再解答:我们已经知道,根据几何图形的面积关系可以说明完全平方公式,实际上还有一些等式也可以用这种方式加以说明,例如:
(2a+b)(a+b)=2a2+3ab+b2,就可以用图①的面积关系来说明.
(1)根据图②写出一个等式: ;
(2)已知等式:(x+p)(x+q)=x2+(p+q)x+pq,请你画出一个相应的几何图形加以说明.
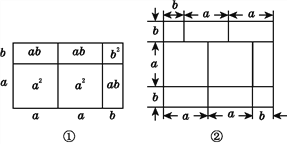
查看答案和解析>>
科目:初中数学 来源: 题型:
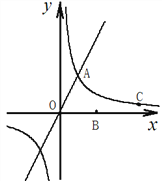
【题目】如图,正比例函数![]() (
(![]() )的图像与反比例函数
)的图像与反比例函数![]() (
(![]() )的图像交于点
)的图像交于点![]() ,且点
,且点![]() 在反比例函数的图像上,点
在反比例函数的图像上,点![]() 的坐标为
的坐标为![]() .
.
(1)求正比例函数![]() 的解析式;
的解析式;
(2)若![]() 为射线
为射线![]() 上一点,①若点
上一点,①若点![]() 的横坐标为
的横坐标为![]() ,
, ![]() 的面积为
的面积为![]() ,写出
,写出![]() 关于
关于![]() 的函数解析式,并指出自变量
的函数解析式,并指出自变量![]() 的取值范围;②当
的取值范围;②当![]() 是等腰三角形时,求点
是等腰三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线L;y=ax2+bx+c(其中a、b、c都不等于0), 它的顶点P的坐标是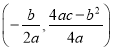 ,与y轴的交点是M(0,c)我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.
,与y轴的交点是M(0,c)我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.
(1)请直接写出抛物线y=2x2-4x+1的伴随抛物线和伴随直线的关系式:
伴随抛物线的关系式_________________
伴随直线的关系式___________________
(2)若一条抛物线的伴随抛物线和伴随直线分别是y=-x2-3和y=-x-3, 则这条抛物线的关系是___________:
(3)求抛物线L:y=ax2+bx+c(其中a、b、c都不等于0) 的伴随抛物线和伴随直线的关系式;
(4)若抛物线L与x轴交于A(x1,0),B(x2,0)两点x2>x1>0,它的伴随抛物线与x 轴交于C,D两点,且AB=CD,请求出a、b、c应满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
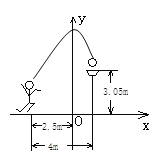
【题目】如图所示,一位篮球运动员在离篮圈水平距离为4m处跳起投篮,球沿一条抛物线运行,当球运行的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心离地面距离为3.05m.
(1)建立如图所示的直角坐标系,求抛物线所对应的函数关系式;
(2)若该运动员身高1.8m,这次跳投时,球在他头顶上方0.25m处出手.问:球出手时,他跳离地面多高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列五个命题:
(1)若直角三角形的两条边长为5和12,则第三边长是13;
(2)如果a≥0,那么![]() =a
=a
(3)若点P(a,b)在第三象限,则点P(﹣a,﹣b+1)在第一象限;
(4)对角线互相垂直且相等的四边形是正方形;
(5)两边及第三边上的中线对应相等的两个三角形全等.
其中不正确命题的个数是( )
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com