练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】先阅读再解答:我们已经知道,根据几何图形的面积关系可以说明完全平方公式,实际上还有一些等式也可以用这种方式加以说明,例如:

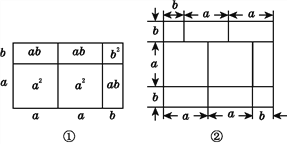
    (2a+b)(a+b)=2a2+3ab+b2,就可以用图①的面积关系来说明.

    (1)根据图②写出一个等式:　　　　　　　　;

    (2)已知等式:(x+p)(x+q)=x2+(p+q)x+pq,请你画出一个相应的几何图形加以说明.

    【答案】(1)(2a+b)(a+2b)=2a2+5ab+2b2(2)图形见解析

    【解析】试题分析：（1）根据所给的长方形面积的两种表示法即可得等式；（2）画一个长为x+p，宽为x+q的长方形即可．

    试题解析：

    (1)(2a+b)(a+2b)=2a2+5ab+2b2　

    (2)如图.(所画图形不唯一)

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列命题中，是真命题的是（ ）

    ①面积相等的两个直角三角形全等；

    ②对角线互相垂直的四边形是正方形；

    ③将抛物线 向左平移4个单位，再向上平移1个单位可得到抛物线 ；

    ④两圆的半径R、r分别是方程x2-3x+2=0 的两根，且圆心距d=3， 则两圆外切.

    A. ① B. ② C. ③ D. ④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某批发商计划将一批海产品由A地运往B地．汽车货运公司和铁路货运公司均开办海产品运输业务．已知运输路程为120千米，汽车和火车的速度分别为60千米／时、100千米／时．两货运公司的收费项目及收费标准如下表所示：

    运输工具

    运输费单价／

    (元／吨·千米)

    冷藏费单价／

    (元／吨·小时)

    过路费／元

    装卸及管理费／元

    汽 车

    2

    5

    200

    0

    火 车

    1.8

    5

    0

    1600

    注：“元／吨·千米”表示每吨货物每千米的运费；“元／吨·小时”表示每吨货物每小时的冷藏费．

    (1)设该批发商待运的海产品有x(吨)，汽车货运公司和铁路货运公司所要收取的费用分别为y1(元)和y2(元)，试求y1、y2与x之间的函数关系式．

    (2)若该批发商待运的海产品不少于30吨，为节省运费，他应选择哪个货运公司承担运输业务?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用分解因式法解方程：

    （1）4x2-12x=0；（2）25x2-9=0；（3）3y2-5y=0；（4）；

    （5）4(x＋3)2-(x-2)2=0 ；（6）4y2+12y+9=0；（7）；

    （8）4(x-3) 2-x(x-3)=0；（9）(x-3)2-2(x-3)+1=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（﹣4，5），（﹣1，3）．

    （1）请在如图所示的网格平面内作出平面直角坐标系；

    （2）请作出△ABC关于y轴对称的△A1B1C1；

    （3）写出点B1的坐标；

    （4）求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（12分）某公交公司有A，B型两种客车，它们的载客量和租金如下表：

    红星中学根据实际情况，计划租用A，B型客车共5辆，同时送七年级师生到基地校参加社会实践活动，设租用A型客车x辆，根据要求回答下列问题：

    （1）用含x的式子填写下表：

    （2）若要保证租车费用不超过1900元，求x的最大值；

    （3）在（2）的条件下，若七年级师生共有195人，写出所有可能的租车方案，并确定最省钱的租车方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，自行车每节链条的长度为2.5cm，交叉重叠部分的圆的直径为0.8cm．

    （1）观察图形填写下表：

    链条节数（节）

    2

    3

    4

    链条长度（cm）

    　 　

    　 　

    　 　

    （2）如果x节链条的总长度是y，求y与x之间的关系式；

    （3）如果一辆某种型号自行车的链条（安装前）由80节这样的链条组成，那么这根链条完成链接（安装到自行车上）后，总长度是多少cm？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料：

    关于，的二元一次方程有一组整数解则方程的全部整数解可表示为（为整数）.

    问题：求方程的所有正整数解.

    小明参考阅读材料，解决该问题如下：

    解：该方程一组整数解为则全部整数解可表示为（为整数）.

    因为解得.因为为整数，所以0或.

    所以该方程的正整数解为和.

    请你参考小明的解题方法， 完成下面的问题：

    （1）方程的全部正整数解为______________；

    （2）方程的全部整数解表示为： （为整数）；

    （3）方程的正整数解有多少组? 请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某商场为了吸引顾客，设立了一个可以自由转动的转盘，并规定：每购买500元商品，就能获得一次转动转盘的机会，如果转盘停止后，指针上对准500、200、100、50、10的区域，顾客就可以获得500元、200元、100元、50元、10元的购物券一张（转盘等分成20份）。

    （1）小华购物450元，他获得购物券的概率是多少？

    （2）小丽购物600元，那么：

    ① 她获得50元购物券的概率是多少？

    ② 她获得100元以上（包括100元）购物券的概率是多少？

    查看答案和解析>>

    同步练习册答案