
【题目】(12分)某公交公司有A,B型两种客车,它们的载客量和租金如下表:

红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地校参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:

(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
【答案】(1)30(5﹣x);280(5﹣x);(2)4;(3)有两种:A型3辆,B型2辆或A型4辆,B型1辆,最省钱的方案是A型3辆,B型2辆.
【解析】
试题分析:(1)由已知有:载客量=汽车辆数×单车载客量,租金=汽车辆数×单车租金,列出代数表达式即可;
(2)由题意,表示出租车总费用,列出不等式即可;
(3)由(2)得出x的取值范围,一一列举计算,排除不合题意方案即可.
试题解析:(1)∵载客量=汽车辆数×单车载客量,租金=汽车辆数×单车租金,∴B型客车载客量=30(5﹣x);B型客车租金=280(5﹣x);故答案为:30(5﹣x);280(5﹣x);
(2)根据题意,400x+280(5﹣x)≤1900,解得:![]() ,∴x的最大值为4;
,∴x的最大值为4;
(3)由(2)可知,![]() ,故x可能取值为0、1、2、3、4,
,故x可能取值为0、1、2、3、4,
①A型0辆,B型5辆,租车费用为400×0+280×5=1400元,但载客量为45×0+30×5=150<195,故不合题意舍去;
②A型1辆,B型4辆,租车费用为400×1+280×4=1520元,但载客量为45×1+30×4=165<195,故不合题意舍去;
③A型2辆,B型3辆,租车费用为400×2+280×3=1640元,但载客量为45×2+30×3=180<195,故不合题意舍去;
④A型3辆,B型2辆,租车费用为400×3+280×2=1760元,但载客量为45×3+30×2=195=195,符合题意;
⑤A型4辆,B型1辆,租车费用为400×4+280×1=1880元,但载客量为45×4+30×1=210,符合题意;
故符合题意的方案有④⑤两种,最省钱的方案是A型3辆,B型2辆.


科目:初中数学 来源: 题型:
【题目】图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是

A. 当x=3时,EC<EM B. 当y=9时,EC>EM
C. 当x增大时,EC·CF的值增大。 D. 当y增大时,BE·DF的值不变。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块直角三角形的绿地,量得两直角边长分别为6 m,8 m,现在要将绿地扩充成等腰三角形,且扩充部分是以8 m为直角边的直角三角形,求扩充后等腰三角形绿地的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
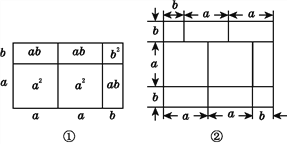
【题目】先阅读再解答:我们已经知道,根据几何图形的面积关系可以说明完全平方公式,实际上还有一些等式也可以用这种方式加以说明,例如:
(2a+b)(a+b)=2a2+3ab+b2,就可以用图①的面积关系来说明.
(1)根据图②写出一个等式: ;
(2)已知等式:(x+p)(x+q)=x2+(p+q)x+pq,请你画出一个相应的几何图形加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用我们学过的知识,可以导出下面这个形式优美的等式:
a2+b2+c2-ab-bc-ac=![]() [(a-b)2+(b-c)2+(c-a)2],
[(a-b)2+(b-c)2+(c-a)2],
该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美.
(1)请你检验这个等式的正确性;
(2)若a=2 016,b=2 017,c=2 018,你能很快求出a2+b2+c2-ab-bc-ac的值吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有5个边长为1的小正方形组成的纸片,可以把它剪拼成一个正方形.
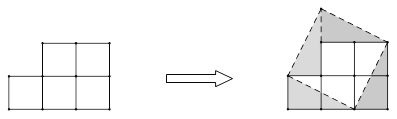
(1) 拼成的正方形的面积是 ,边长是 ;
(2) 在数轴上作出表示![]() 、-2
、-2![]() 的点;
的点;
(3) 你能把这十个小正方形组成的图形纸,剪开并拼成一个大正方形吗?若能,在图中画出拼接后的正方形,并求边长,若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC与Rt△ABD中,∠ABC=∠BAD=90°,AD=BC,AC,BD相交于点G,过点A作AE∥DB交CB的延长线于点E,过点B作BF∥CA交DA的延长线于点F,AE,BF相交于点H.
(1)图中有若干对三角形是全等的,请你任选一对进行证明;(不添加任何辅助线)
(2)证明:四边形AHBG是菱形;
(3)若使四边形AHBG是正方形,还需在Rt△ABC的边长之间再添加一个什么条件?请你写出这个条件.(不必证明)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com