
【题目】如图①,AB是⊙O的直径,且AB=10,C是⊙O上的动点,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D.(1)求证:∠DAC=∠BAC;
(2)若AD和⊙O相切于点A,求AD的长;
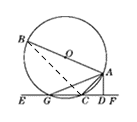
(3)若把直线EF向上平行移动,如图②,EF交⊙O于G,C两点,题中的其他条件不变,试问这时与∠DAC相等的角是否存在,并说明理由.

【答案】(1)详见解析;(2)5;(3)存在,∠BAG=∠DAC,理由详见解析.
【解析】试题分析:
(1)连接OC,则OC∥AD,得∠OCA=∠DAC,又∠OCA=∠OAC,即可证明;
(2)根据切线长定理,证明矩形OADC是正方形;
(3)连接BC,证∠BCG=∠DAC,又∠BCG=∠BAG,即得证.
试题解析:
(1)证明:如图①,连接OC.∵直线EF和⊙O相切于点C,
∴OC⊥EF.∵AD⊥EF,∴OC∥AD.∴∠DAC=∠OCA.
∵OA=OC,∴∠BAC=∠OCA.∴∠DAC=∠BAC.
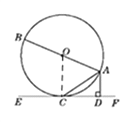
(2)解:∵AD和⊙O相切于点A,∴OA⊥AD.∵AD⊥EF,OC⊥EF,
∴∠OAD=∠ADC=∠OCD=90°.∴四边形OADC是矩形.∵OA=OC,
∴矩形OADC是正方形.∴AD=OA.∵AB=2OA=10,∴AD=OA=5.
(3)解:存在,∠BAG=∠DAC.理由如下:如图,连接BC.∵AB是⊙O的直径,
∴∠BCA=90°.∴∠ACD+∠BCG=90°.∵∠ADC=90°,
∴∠ACD+∠DAC=90°.∴∠DAC=∠BCG.∵∠BCG=∠BAG,∴∠BAG=∠DAC.


科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如下表:
甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
且![]() =8,
=8, ![]() =1.8.根据上述信息完成下列问题:
=1.8.根据上述信息完成下列问题:
(1)将甲运动员的折线统计图补充完整.
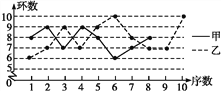
(2)求乙运动员射击训练成绩的众数和中位数.
(3)求甲运动员射击成绩的平均数和方差,并判断甲、乙两人本次射击成绩的稳定性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )

A. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B. 一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C. 暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D. 掷一个质地均匀的正六面体骰子,向上的面点数是4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x+4
(1)在如图所示的平面直角坐标系中,画出函数的图象;

2)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出:当y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=mx2-(m+5)x+5.
(1)求证:它的图象与x轴必有交点,且过x轴上一定点;
(2)这条抛物线与x轴交于两点A(x1,0),B(x2,0),且0<x1<x2,过(1) 中定点的直线L;y=x+k交y轴于点D,且AB=4,圆心在直线L上的⊙M为A、B两点,求抛物线和直线的关系式,弦AB与弧![]() 围成的弓形面积.
围成的弓形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
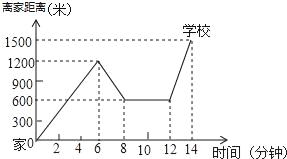
(1)小明家到学校的路程是多少米?
(2)小明在书店停留了多少分钟?
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
(4)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
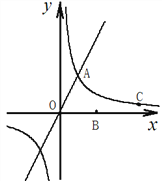
【题目】如图,正比例函数![]() (
(![]() )的图像与反比例函数
)的图像与反比例函数![]() (
(![]() )的图像交于点
)的图像交于点![]() ,且点
,且点![]() 在反比例函数的图像上,点
在反比例函数的图像上,点![]() 的坐标为
的坐标为![]() .
.
(1)求正比例函数![]() 的解析式;
的解析式;
(2)若![]() 为射线
为射线![]() 上一点,①若点
上一点,①若点![]() 的横坐标为
的横坐标为![]() ,
, ![]() 的面积为
的面积为![]() ,写出
,写出![]() 关于
关于![]() 的函数解析式,并指出自变量
的函数解析式,并指出自变量![]() 的取值范围;②当
的取值范围;②当![]() 是等腰三角形时,求点
是等腰三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.
正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN—∠AMB
=180°—∠B—∠AMB
=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正![]() 边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)


图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com