【题目】如图，已知：∠BCF=∠B+∠F.求证：AB//EF .
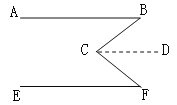
证明：经过点C作CD//AB
∴∠BCD=∠B.（ ）
∵∠BCF=∠B+∠F，（已知）
∴∠ （ ）=∠F.（ ）
∴CD//EF.（ ）
∴AB//EF（ ）
科目：初中数学 来源： 题型：
【题目】计算：
(1)－23＋
(2 018＋3)0－
； (2)992－69×71；
(3) 
÷(－3xy); (4)(－2＋x)(－2－x)；
(5)(a＋b－c)(a－b＋c); (6)(3x－2y＋1)2.
查看答案和解析>>
科目：初中数学 来源： 题型：
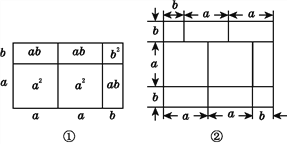
【题目】先阅读再解答:我们已经知道,根据几何图形的面积关系可以说明完全平方公式,实际上还有一些等式也可以用这种方式加以说明,例如:
(2a+b)(a+b)=2a2+3ab+b2,就可以用图①的面积关系来说明.
(1)根据图②写出一个等式: ;
(2)已知等式:(x+p)(x+q)=x2+(p+q)x+pq,请你画出一个相应的几何图形加以说明.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线L;y=ax2+bx+c(其中a、b、c都不等于0), 它的顶点P的坐标是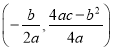
,与y轴的交点是M(0,c)我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.
(1)请直接写出抛物线y=2x2-4x+1的伴随抛物线和伴随直线的关系式:
伴随抛物线的关系式_________________
伴随直线的关系式___________________
(2)若一条抛物线的伴随抛物线和伴随直线分别是y=-x2-3和y=-x-3, 则这条抛物线的关系是___________:
(3)求抛物线L:y=ax2+bx+c(其中a、b、c都不等于0) 的伴随抛物线和伴随直线的关系式;
(4)若抛物线L与x轴交于A(x1,0),B(x2,0)两点x2>x1>0,它的伴随抛物线与x 轴交于C,D两点,且AB=CD,请求出a、b、c应满足的条件.
查看答案和解析>>
科目：初中数学 来源： 题型：
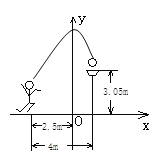
【题目】如图所示,一位篮球运动员在离篮圈水平距离为4m处跳起投篮,球沿一条抛物线运行,当球运行的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心离地面距离为3.05m.
(1)建立如图所示的直角坐标系,求抛物线所对应的函数关系式;
(2)若该运动员身高1.8m,这次跳投时,球在他头顶上方0.25m处出手.问:球出手时,他跳离地面多高?
查看答案和解析>>
科目：初中数学 来源： 题型：
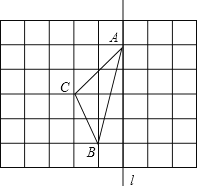
【题目】如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．
（1）在图中画出与关于直线
成轴对称的△A′B′C′；
（2）线段CC′被直线
；
（3）△ABC的面积为 ；
（4）在直线
上找一点P，使PB+PC的长最短．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列五个命题：
（1）若直角三角形的两条边长为5和12，则第三边长是13；
（2）如果a≥0，那么
=a
（3）若点P（a，b）在第三象限，则点P（﹣a，﹣b+1）在第一象限；
（4）对角线互相垂直且相等的四边形是正方形；
（5）两边及第三边上的中线对应相等的两个三角形全等．
其中不正确命题的个数是（ ）
A．2个 B．3个 C．4个 D．5个
查看答案和解析>>
科目：初中数学 来源： 题型：
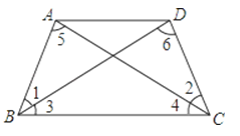
【题目】如图，已知∠3=∠4，要说明△ABC≌△DCB，
（1）若以“SAS”为依据，则需添加一个条件是________
（2）若以“AAS”为依据，则需添加一个条件是________
（3）若以“ASA”为依据，则需添加一个条件是________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
