练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    某体育用品专卖店销售7个篮球和9个排球的总利润为355元，销售10个篮球和20个排球的总利润为650元．

    （1）求每个篮球和每个排球的销售利润；

    （2）已知每个篮球的进价为200元，每个排球的进价为160元，若该专卖店计划用不超过17400元购进篮球和排球共100个，且要求篮球数量不少于排球数量的一半，请你为专卖店设计符合要求的进货方案．


    解：（1）设每个篮球和每个排球的销售利润分别为x元，y元，

    根据题意得：，

    解得：，

    答：每个篮球和每个排球的销售利润分别为25元，20元；

    （2）设购进篮球m个，排球（100﹣m）个，

    根据题意得：，

    解得：≤m≤35，

    ∴m=34或m=35，

    ∴购进篮球34个排球66个，或购进篮球35个排球65个两种购买方案．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


               .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


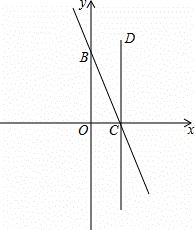
    如图，直线y=﹣2x+4与坐标轴分别交于C、B两点，过点C作CD⊥x轴，点P是x轴下方直线CD上的一点，且△OCP与△OBC相似，求过点P的双曲线解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    的平方根是　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：（﹣2）0+（）﹣1+4cos30°﹣|﹣|

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，直线a，b被直线c所截，且a∥b，∠1=40°，则∠2=　　度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列运算正确的是（　　）

    　   A．a+2a=2a2          B． +=          C．                             （x﹣3）2=x2﹣9    D． （x2）3=x6

    查看答案和解析>>

    科目：初中数学 来源： 题型：


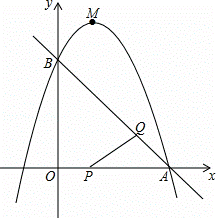
    如图，已知直线y=﹣x+3与x轴、y轴分别交于A，B两点，抛物线y=﹣x2+bx+c经过A，B两点，点P在线段OA上，从点O出发，向点A以1个单位/秒的速度匀速运动；同时，点Q在线段AB上，从点A出发，向点B以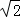个单位/秒的速度匀速运动，连接PQ，设运动时间为t秒．

    （1）求抛物线的解析式；

    （2）问：当t为何值时，△APQ为直角三角形；

    （3）过点P作PE∥y轴，交AB于点E，过点Q作QF∥y轴，交抛物线于点F，连接EF，当EF∥PQ时，求点F的坐标；

    （4）设抛物线顶点为M，连接BP，BM，MQ，问：是否存在t的值，使以B，Q，M为顶点的三角形与以O，B，P为顶点的三角形相似？若存在，请求出t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    为了丰富学生的体育生活，学校准备购进一些篮球和足球，已知用900元购买篮球的个数比购买足球的个数少1个，足球的单价为篮球单价的0.9倍．

    （1）求篮球、足球的单价分别为多少元？

    （2）如果计划用5000元购买篮球、足球共52个，那么至少要购买多少个足球？

    查看答案和解析>>

    同步练习册答案