
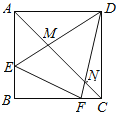
【题目】如图,已知正方形![]() 中,
中,![]() 为对角线,点
为对角线,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,
上,![]() ,
,![]() 、
、![]() 与
与![]() 分别交于点
分别交于点![]() 、
、![]() ,
,![]() ,
,![]() ,则
,则![]() __.
__.
【答案】![]()
【解析】
延长EA至H,使AH=CF,连结DH,证明△DCF≌△DAH,得∠CDF=∠ADH,证明△HDE≌△FDE,则∠EDF=45°,将△ADM绕点D逆时针旋转90°,使DA边与DC边重合,得到△DCQ,根据SAS判定△DMN≌△DQN,可得MN=NQ,∠NCQ=90°,则NQ可求出.
解:延长EA至H,使AH=CF,连结DH,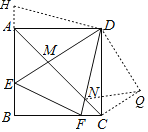
在Rt△DCF和Rt△DAH中,
∵AH=CF,AD=CD,∠HAD=∠FCD=90°,
∴Rt△DCF≌Rt△DAH(SAS),
∴∠CDF=∠ADH,DH=DF,
∵AE+FC=EF,
∴EF=EH,
∵DE=DE,
∴△HDE≌△FDE(SSS),
∴∠HDE=∠FDE,
∴∠EDF=![]() ∠ADC=45°,
∠ADC=45°,
将△ADM绕点D逆时针旋转90°,使DA边与DC边重合,得到△DCQ,连结NQ,
由旋转可得,△ADM≌△DCQ,
∴AM=CQ,∠ADM=∠CDQ,
∵∠EDF=45°,∠ADC=90°,
∴∠ADM+∠FDC=45°,
∴∠CDQ+∠FDC=45°,即∠NDQ=45°,
在△DMN和△DQN中,
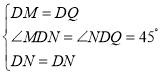
∴△DMN≌△DQN(SAS),
∴MN=NQ,
又∠NCQ=∠NCD+∠DCQ=45°+45°=90°,
在Rt△NCQ中,NQ2=CQ2+NC2,即MN2=AM2+NC2
∵AM=4,NC=2,
∴![]()
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】某商店销售一种玩具,每件的进货价为40元.经市场调研,当该玩具每件的销售价为50元时,每天可销售200件;当每件的销售价每增加1元,每天的销售数量将减少10件,现该商店决定涨价销售.
(1)当每件的销售价为53元,该玩具每天的销售数量为 件;
(2)若商店销售该玩具每天获利2000元,每件玩具销售价应定为多少元?
(3)若该玩具每件销售价不低于57元,同时,每天的销售量至少20件,求每件的销售价定为多少元时,销售该玩具每天获得的利润w最大?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,以点C(2,![]() )为圆心,以2为半径的圆与x轴交于A,B两点.
)为圆心,以2为半径的圆与x轴交于A,B两点.
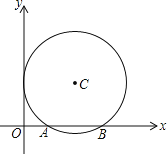
(1)求A,B两点的坐标;
(2)若二次函数y=x2+bx+c的图象经过点A,B,试确定此二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,其部分图象如图所示则下列结论:①4a﹣b=0;②c<0;③c>3a;④4a﹣2b>at2+bt(t为实数);⑤点(﹣![]() ,y1),(﹣
,y1),(﹣![]() ,y2),(
,y2),(![]() )是该抛物线上的点,则y2<y1<y3,其中,正确结论的个数是( )
)是该抛物线上的点,则y2<y1<y3,其中,正确结论的个数是( )
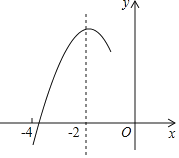
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运动员将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间t(s)满足二次函数关系,t与h的几组对应值如下表所示.
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度;
(3)问:小球的飞行高度能否达到22m?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com