
����Ŀ��ij�̵�����һ����ߣ�ÿ���Ľ�����Ϊ40Ԫ�����г����У��������ÿ�������ۼ�Ϊ50Ԫʱ��ÿ�������200������ÿ�������ۼ�ÿ����1Ԫ��ÿ�����������������10�����ָ��̵�����Ǽ����ۣ�
��1����ÿ�������ۼ�Ϊ53Ԫ�������ÿ�����������Ϊ�� ������
��2�����̵����۸����ÿ�����2000Ԫ��ÿ��������ۼ�Ӧ��Ϊ����Ԫ��
��3���������ÿ�����ۼ۲�����57Ԫ��ͬʱ��ÿ�������������20������ÿ�������ۼ۶�Ϊ����Ԫʱ�����۸����ÿ���õ�����w�������������
���𰸡���1��170��
��2�����̵����۸����ÿ�����2000Ԫ��ÿ��������ۼ�Ӧ��Ϊ60Ԫ��
��3��ÿ�������ۼ۶�Ϊ57Ԫʱ�����۸����ÿ���õ�����w����������Ϊ2210��
��������
��1�����ݵ�����������20010�����ӵ����۵��ۣ�����������ۣ�
��2����ü���Ʒ�����۵���ΪxԪ��x��40���������������Ϊ20010��x50���������ݵ������������ÿ������������������������ɵó�����x��һԪ���η��̣���֮ȡ��ϴ�ֵ���ɵó����ۣ�
��3��ֱ�����õ������������ÿ����������������������ó�������ϵʽ���������ֵ���ɣ�
�⣺��1��200����53��50����10��170��������
�𣺸����ÿ�����������Ϊ170����
�ʴ�Ϊ��170��
��2����ÿ��������ۼ�Ӧ��ΪxԪ��
����������x��40��[200��10��x��50��]��2000��
��ã�x1��50��x2��60��
���̵�����Ǽ����ۣ�
��x��60��
�����̵����۸����ÿ�����2000Ԫ��ÿ��������ۼ�Ӧ��Ϊ60Ԫ��
��3����ÿ�������ۼ۶�ΪxԪ����������ã����ۼ�Ӧ���������Ϊ![]() ��
��
��ã�57��x��68��
������ã�w����x��40��[200��10��x��50��]
����10x2+1100x��28000����10��x��55��2+2250��
����10��0�������ߵĿ������£��Գ���Ϊֱ��x��55��
����57��x��68ʱ��w��x���������С��
����x��57ʱ��w�������10��57��55��2+2250��2210��
��ÿ�������ۼ۶�Ϊ57Ԫʱ�����۸����ÿ���õ�����w����������Ϊ2210��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
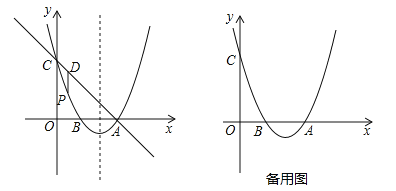
����Ŀ����֪��ͼ��������y=x2+bx+c����A��3��0����B��1��0������y���ڵ�C����P�Ǹ���������һ���㣬��P��C������������A���˶�����P�����A�غϣ�������P��PD��y�ύֱ��AC�ڵ�D��
��1���������ߵĽ���ʽ��
��2�����P���˶��Ĺ������߶�PD���ȵ����ֵ��
��3����APD�ܷ�ֱ�������Σ�������ֱ��д����P���꣬��������˵�����ɣ�
��4���������߶Գ������Ƿ���ڵ�Mʹ|MA��MC|����������������M�����꣬����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
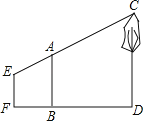
����Ŀ����ͼ��Ϊ�˲���һ����CD�ĸ߶ȣ���������B������һ����Ϊ2.5m�ı�ˣ��۲��ߴ�E�����Կ����˶�A������C��ͬһ��ֱ���ϣ������BD��7m��FB��3m��EF��1.6m��������Ϊ_____m��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
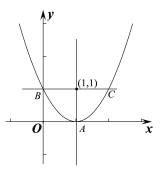
����Ŀ�������κ���y=|a|x2+bx+c��ͼ��A(m,n)��B(0,y1)��C(3��m,n)��D(![]() , y2)��E(2,y3)����y1��y2��y3�Ĵ�С��ϵ��( ).
, y2)��E(2,y3)����y1��y2��y3�Ĵ�С��ϵ��( ).
A. y1< y2< y3B. y1 < y3< y2C. y3< y2< y1D. y2< y3< y1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y=ax2+bx+c(b<0)����ֻ��һ��������.
(1)������������Ϊ(2��0)����a��c����Ĺ�ϵʽ��
(2)��AΪ�������ϵ�һ���㣬ֱ��l��y=kx+1��k�������߽��ڵ�B��C���㣬ֱ��BD��ֱ��ֱ��y=��1,����Ϊ��D.��k��0ʱ��ֱ��l�������ߵ�һ��������y���ϣ�����ABCΪ����ֱ��������.
�����A������������ߵĽ���ʽ��
��֤��������ÿ��������ʵ��k������A��D��C���㹲��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+2������A(��1��0)��B(4��0)����y���ڵ�C��
(1)�������ߵĽ���ʽ��
(2)��DΪy���Ҳ���������һ�㣬�Ƿ���ڵ�D��ʹS��ABC��S��ABD�������ڣ��������D���꣺�������ڣ���˵������.
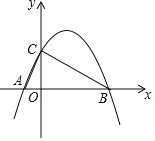
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�Ҫ��Ӫһ�������е��ľߣ�����Ϊ20Ԫ����Ӫ���η��֣������۵�����25Ԫʱ��ÿ���������Ϊ250�������۵���ÿ����1Ԫ��ÿ����������ͼ���10����
��1��д���̳����������ľߣ�ÿ�����õ���������![]() ��Ԫ�������۵���
��Ԫ�������۵���![]() ��Ԫ��֮��ĺ�����ϵʽ��
��Ԫ��֮��ĺ�����ϵʽ��
��2�������۵���Ϊ����Ԫʱ�����ľ�ÿ�����������������ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BE�ǡ�O��ֱ�����뾶OA����BC������ΪD������AE��EC��

��1������AEC��25�������AOB�Ķ�����
��2������A����B��EC��4�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
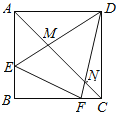
����Ŀ����ͼ����֪������![]() �У�
�У�![]() Ϊ�Խ��ߣ���
Ϊ�Խ��ߣ���![]() �ڱ�
�ڱ�![]() �ϣ���
�ϣ���![]() �ڱ�
�ڱ�![]() �ϣ�
�ϣ�![]() ��
��![]() ��
��![]() ��
��![]() �ֱ��ڵ�
�ֱ��ڵ�![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() __��
__��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com