
����Ŀ����֪����y=ax2+bx+c(b<0)����ֻ��һ��������.
(1)������������Ϊ(2��0)����a��c����Ĺ�ϵʽ��
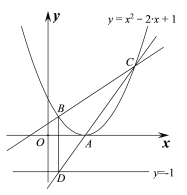
(2)��AΪ�������ϵ�һ���㣬ֱ��l��y=kx+1��k�������߽��ڵ�B��C���㣬ֱ��BD��ֱ��ֱ��y=��1,����Ϊ��D.��k��0ʱ��ֱ��l�������ߵ�һ��������y���ϣ�����ABCΪ����ֱ��������.
�����A������������ߵĽ���ʽ��
��֤��������ÿ��������ʵ��k������A��D��C���㹲��.
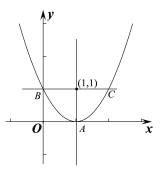
���𰸡�(1) y=a(x��2)2, c=4a;(2) �ٶ���A(1,0)��y= x2��2x+1,�ڼ�����.
��������
��1��������������x��Ĺ��������꼴Ϊ�����������꣬������⣻
��2����y��kx��1k��k��x1����1�����㣨1��1�����ҵ�k��0ʱ��ֱ��l��Ϊy��1ƽ��x�ᣬ����Ľ���Ϊ��0��1����������⣻�ڼ���ֱ��AD����ʽ�е�kֵ��ֱ��AC����ʽ�е�kֵ������kֵ��ȼ�����⣮
�⣺��1����������x��Ĺ��������꼴Ϊ�����������꣬�ʣ�y��a��x2��2����c��4a��
(2) y=kx+1��k= k(x��1)+1������(1,1),
�ҵ�k��0ʱ��ֱ��l��Ϊy=1ƽ��x��,��y��Ľ���Ϊ(0,1)
����ABCΪ����ֱ�������Σ����AΪ�����ߵĶ���
��c=1������A(1,0)
�����ߵĽ���ʽ: y= x2��2x+1.
��![]()
x2��(2+k)x+k��0,
x��![]() (2+k��
(2+k��![]() )
)
xD��xB��![]() (2+k��
(2+k��![]() ), yD=��1��
), yD=��1��
��D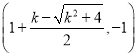
yC��![]() (2+k2+k
(2+k2+k![]() ,
,
C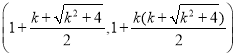 ��A(1,0)
��A(1,0)
��ֱ��AD����ʽ�е�kֵΪ��k AD=![]() =
=![]() ��
��
ֱ��AC����ʽ�е�kֵΪ��k AC=![]()
��k AD= k AC, ��A��C��D���㹲��.


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⷽ�̣�
��1��x2��7��4x��
��2��x2��2x��
��3��x2��6x+9����5��2x��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
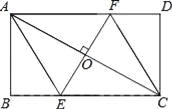
����Ŀ����ͼ��AC�Ǿ���ABCD�ĶԽ��ߣ���AC���е�O��EF��AC����BC�ڵ�E����AD�ڵ�F������AE��CF��
��1����֤���ı���AECF�����Σ�
��2����AB=![]() ����DCF=30�������ı���AECF�������������������ţ�
����DCF=30�������ı���AECF�������������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������8�֣���֪��ABC������AB��AC�ij�ǡ���ǹ���x�ķ���x2��(2k��3)x��k2��3k��2��0������ʵ������������BC�ij�Ϊ5
(1) ��֤��AB��AC
(2) �����ABC����BCΪб�ߵ�ֱ�������Σ���k��ֵ
(3) ��գ���k��________ʱ����ABC�ǵ��������Σ���ABC���ܳ�Ϊ________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ��ÿ��С�����εı߳���Ϊ1����λ���ȣ���A��B���ڸ���ϣ����������ߵĽ���и�㣩��
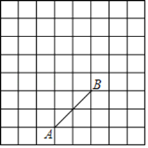
��1�����߶�AB����ƽ��������λ���ȣ���A�Ķ�Ӧ��Ϊ��A1����B�Ķ�Ӧ��Ϊ��B1���뻭��ƽ�ƺ���߶�A1B1��
��2�����߶�A1B1�Ƶ�A1����ʱ�뷽����ת90������B1�Ķ�Ӧ��Ϊ��B2���뻭����ת����߶�A1B2��
��3������AB2��BB2�����ABB2�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵�����һ����ߣ�ÿ���Ľ�����Ϊ40Ԫ�����г����У��������ÿ�������ۼ�Ϊ50Ԫʱ��ÿ�������200������ÿ�������ۼ�ÿ����1Ԫ��ÿ�����������������10�����ָ��̵�����Ǽ����ۣ�
��1����ÿ�������ۼ�Ϊ53Ԫ�������ÿ�����������Ϊ�� ������
��2�����̵����۸����ÿ�����2000Ԫ��ÿ��������ۼ�Ӧ��Ϊ����Ԫ��
��3���������ÿ�����ۼ۲�����57Ԫ��ͬʱ��ÿ�������������20������ÿ�������ۼ۶�Ϊ����Ԫʱ�����۸����ÿ���õ�����w�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB��90��������ABC�ƶ���C��ʱ����ת�õ���A'B'C��M��BC���е㣬P��A'B'���е㣬����PM����BC��2����BAC��30�������߶�PM�����ֵ�ǣ�������

A.4B.3C.2D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
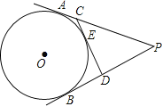
����Ŀ����ͼ��PΪ��O��һ�㣬PA��PB�ֱ��С�O��A��B��CD�С�O�ڵ�E���ֱ�PA��PB�ڵ�C��D������PCD���ܳ�Ϊ24����O�İ뾶��5�����P��Բ��O�ľ���_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���![]() �У�
��![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() �е㣬����
�е㣬����![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
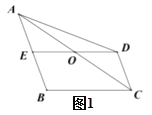
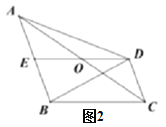
��1����ͼ1����֤��![]() ��
��
��2����ͼ2������![]() ����ֱ��д��ͼ���������
����ֱ��д��ͼ���������![]() ���2���������Σ�
���2����������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com