
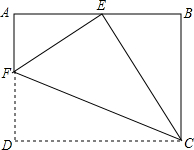
 如图,将一张矩形纸片ABCD沿CF折叠,使点D与AB的中点E重合,求$\frac{AF}{FD}$.
如图,将一张矩形纸片ABCD沿CF折叠,使点D与AB的中点E重合,求$\frac{AF}{FD}$. 分析 根据折叠的性质DF=EF,CE=CD,因为∠FEC=∠D=90°,易证明△AFE∽△BEC,得到AF与EF的比等于BE与EC的比,因为AE=BE=$\frac{1}{2}$AB,所以AF与FD的比等于$\frac{1}{2}$.
解答 解:根据折叠的性质DF=EF,CE=CD,∠FEC=∠D=90°
∴∠AEF+∠BEC=90°
∵∠AEF+∠AFE=90°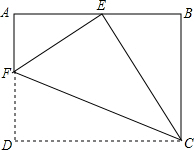
∴∠BEC=∠AFE
又∵∠A=∠B=90°
∴△AFE∽△BEC
∴$\frac{AF}{EF}=\frac{EB}{EC}$
∵E是AB的中点
∴BE=$\frac{1}{2}$AB=$\frac{1}{2}$EC
∴$\frac{AF}{FD}=\frac{AF}{EF}=\frac{\frac{1}{2}EC}{EC}=\frac{1}{2}$.
点评 本题考查了折叠的性质和相似三角形的判定与性质的综合运用,根据折叠的性质和点D与AB的中点E重合,恰当的进行等量代换是解决问题的关键.


科目:初中数学 来源: 题型:解答题
 以下两题任选其一作答:
以下两题任选其一作答:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
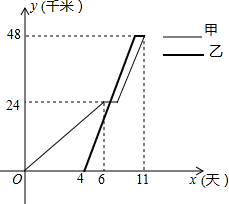 甲、乙两工程队维修同样长度的两段公路,甲队每天完成a千米,中间因故停工一段时间,之后又以每天2a千米的速度继续工作;乙队在甲队工作4天后开始工作,比甲队早一天完成任务.设甲、乙两工程队各自完成任务的工作量为y(千米),甲队的工作时间为x(天).当0≤x≤11时,y与x之间的函数图象如图所示.
甲、乙两工程队维修同样长度的两段公路,甲队每天完成a千米,中间因故停工一段时间,之后又以每天2a千米的速度继续工作;乙队在甲队工作4天后开始工作,比甲队早一天完成任务.设甲、乙两工程队各自完成任务的工作量为y(千米),甲队的工作时间为x(天).当0≤x≤11时,y与x之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
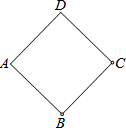 如图,正方形ABCD,边长AB=2.
如图,正方形ABCD,边长AB=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
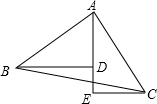 如图,A、D、E三点在同一条直线上,且△BAD≌△ACE.
如图,A、D、E三点在同一条直线上,且△BAD≌△ACE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
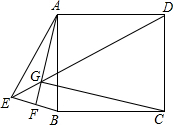 已知E是正方形ABCD外一点,且AB=AE,连BE作AF⊥BE,垂足为F,连DE交AF于G.
已知E是正方形ABCD外一点,且AB=AE,连BE作AF⊥BE,垂足为F,连DE交AF于G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
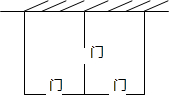 某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门.已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为75m2.
某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门.已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为75m2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
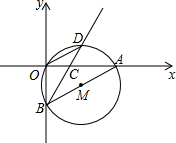 如图,在直角坐标系中,⊙M经过原点O(0,0),点A($\sqrt{6}$,0)与点B(0,-$\sqrt{2}$),点D在劣弧$\widehat{OA}$上,连接BD交x轴于点C,且∠COD=∠CBO.
如图,在直角坐标系中,⊙M经过原点O(0,0),点A($\sqrt{6}$,0)与点B(0,-$\sqrt{2}$),点D在劣弧$\widehat{OA}$上,连接BD交x轴于点C,且∠COD=∠CBO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com