
【题目】在△ABC中,AB=AC,D是线段BC的延长线上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图,点D在线段BC的延长线上移动,若∠BAC=40![]() ,则∠DCE=
,则∠DCE= ![]() .
.
(2)设∠BAC=m,∠DCE=n.
①如图,当点D在线段BC的延长线上移动时,m与n之间有什么数量关系?请说明理由.
②当点D在直线BC上(不与B、C重合)移动时,m与n之间有什么数量关系?请直接写出你的结论.

【答案】(1)40;(2)①m=n,理由见解析;②m+n=180°
【解析】试题分析:(1)可证△ABD≌△ACE,可得∠ACE=∠B,即可解题;
(2)①根据△ABD≌△ACE可分别求得∠BCE用m和用n分别表示,即可求得m、n的关系;②分两种情况分析,第1种,当D在线段BC的延长线上或反向延长线上时,第2种,当D在线段BC上时.
试题解析:(1)∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
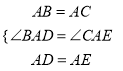 ,
,
∴△ABD≌△ACE(SAS),
∴∠ACE=∠B,
∵AB=AC,∠BAC=40°,
∴∠ACE=∠B=70°,
∴∠DCE=180°70°70°=40°;
(2) ①∵△ABD≌△ACE(1)已证,
∴∠ACE=∠B,
∵AB=AC,∠BAC=m,
∴∠ACE=∠B=∠ACB=![]() ,
,
∴∠BCE=∠ACB+∠ACE=180°m,
∵∠BCE=180°∠DCE=180°n,
∴m=n.
②当D在线段BC的延长线上或反向延长线上时,m=n,
当D在线段BC上时,m+n=180°.


科目:初中数学 来源: 题型:
【题目】阅读下面材料,并解答问题.
将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母为x2-1,可设x4+x2-3=(x2-1)(x2+a)+b.
则x4+x2-3=(x2-1)(x2+a)+b=x4-x2+ax2-a+b=x4+(a-1)x2-a+b
∴![]() ,∴
,∴![]()
∴![]()
这样,分式![]() 被拆分成了一个整式x2+2与一个分式-
被拆分成了一个整式x2+2与一个分式-![]() 的和.
的和.
根据上述作法,将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式。
拆分成一个整式与一个分式(分子为整数)的和的形式。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个正比例函数图象与一个一次函数图象交于点A(3,4),且一次函数的图象与y轴相交于点B(0,-5).

(1)求这两个函数的表达式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() ,(k为常数,k≠1).
,(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而增大,求k的取值范围;
(3)若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
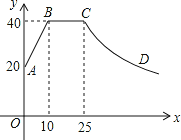
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指数y随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)求出线段AB,曲线CD的解析式,并写出自变量的取值范围;
(2)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+1与y轴交于A点,与反比例函数![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且![]() .
.
(1)求k的值;
(2)设点N(1,a)是反比例函数![]() (x>0)图象上的点,在y轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在y轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求![]() 的长(结果保留π).
的长(结果保留π).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com