
分析 (1)由四张质地、形状、大小完全相同的卡片,它们的正面分别写有-2,$\sqrt{3}$,$\frac{1}{2}$,π,无理数:$\sqrt{3}$,π,直接利用概率公式求解即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两人获胜的情况,再利用概率公式即可求得答案.
解答 解:(1)∵四张质地、形状、大小完全相同的卡片,它们的正面分别写有-2,$\sqrt{3}$,$\frac{1}{2}$,π,无理数:$\sqrt{3}$,π,
∴从中随机抽取一张卡片,是无理数的概率为:$\frac{2}{4}$=$\frac{1}{2}$;
故答案为:$\frac{1}{2}$;
(2)列表得:
| 小红 | -2 | $\sqrt{3}$ | $\frac{1}{2}$ | π |
| -2 | (-2,$\sqrt{3}$) | (-2,$\frac{1}{2}$) | (-2,π) | |
| $\sqrt{3}$ | ($\sqrt{3}$,-2) | ($\sqrt{3}$,$\frac{1}{2}$) | ($\sqrt{3}$,π) | |
| $\frac{1}{2}$ | ($\frac{1}{2}$,-2) | ($\frac{1}{2}$,$\sqrt{3}$) | ($\frac{1}{2}$,π) | |
| π | (π,-2) | (π,$\sqrt{3}$) | (π,$\frac{1}{2}$) |
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.239×105m | B. | 2.39×105m | C. | 2.39×104m | D. | 23.9×103m |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 甲 | 乙 | 丙 | 丁 | |
| 平均数/环 | 9.7 | 9.5 | 9.5 | 9.7 |
| 方差/环2 | 5.1 | 4.7 | 4.5 | 4.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
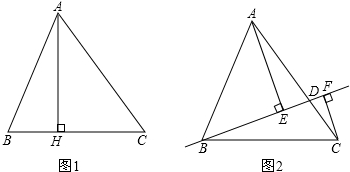
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
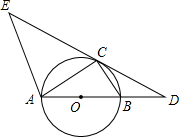 如图,AB是⊙O的直径,点C在⊙O上,∠DCB=∠CAB,AE∥BC,AE交DC的延长线于点E.
如图,AB是⊙O的直径,点C在⊙O上,∠DCB=∠CAB,AE∥BC,AE交DC的延长线于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com