
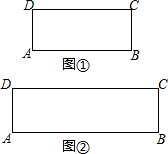
 如果一个点与另外两个点能构成直角三角形,则称这个点为另外两个点的勾股点.例如:矩形ABCD中,点C与A、B两点可构成直角三角形ABC,则称点C为A、B两点的勾股点,同样,点D也是A、B两点的勾股点.
如果一个点与另外两个点能构成直角三角形,则称这个点为另外两个点的勾股点.例如:矩形ABCD中,点C与A、B两点可构成直角三角形ABC,则称点C为A、B两点的勾股点,同样,点D也是A、B两点的勾股点.分析 (1)作线段DC的垂直平分线,垂直平分线与DC的交点即为所求作的点;
(2)由∠APB=90°,可证明∠DAP=CPB,由∠D=∠C可知证明△DPA∽△BCP,由相似三角形的性质可知$\frac{DP}{AD}=\frac{CB}{PC}$,设DP=x,则PC=3-x,则$\frac{x}{1}=\frac{1}{3-x}$,从而可解得x的值.
解答 解:(1)如图所示:点E即为所求.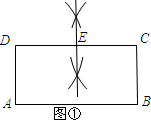
(2)如图②所示:
∵△ABP为直角三角形,
∴∠APB=90°.
∴∠DPA+∠CPB=90°.
∵∠DAP+APD=90°,
∴∠DAP=CPB.
又∵∠D=∠C,
∴△DPA∽△BCP.
∴$\frac{DP}{AD}=\frac{CB}{PC}$.
设DP=x,则PC=3-x,则$\frac{x}{1}=\frac{1}{3-x}$.
解得:x=$\frac{3±\sqrt{5}}{2}$.
∴DP=$\frac{3±\sqrt{5}}{2}$.
点评 本题主要考查的是作图应用与设计、相似三角形的性质和判定,根据相似三角形的性质得到关于x的方程是解题的关键.


科目:初中数学 来源: 题型:解答题
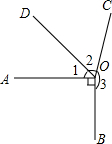 (1)从点O引四条射线OA,OB,OC,OD,如果∠AOB:∠BOC:∠COD:∠DOA=1:2:3:4,那么这四个角的度数分别是多少?
(1)从点O引四条射线OA,OB,OC,OD,如果∠AOB:∠BOC:∠COD:∠DOA=1:2:3:4,那么这四个角的度数分别是多少?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
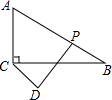 如图,在Rt△ABC中.∠ACB=90°,∠B=30°,CB=3$\sqrt{3}$,点D是平面上一点且CD=2,点P为线段AB上一动点.当△ABC绕点C任意旋转时,在旋转过程中线段DP长度的最大值为2+3$\sqrt{3}$,最小值为$\frac{3\sqrt{3}}{2}$-2.
如图,在Rt△ABC中.∠ACB=90°,∠B=30°,CB=3$\sqrt{3}$,点D是平面上一点且CD=2,点P为线段AB上一动点.当△ABC绕点C任意旋转时,在旋转过程中线段DP长度的最大值为2+3$\sqrt{3}$,最小值为$\frac{3\sqrt{3}}{2}$-2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m$>\frac{1}{2}$ | B. | m=$\frac{1}{2}$ | C. | m$<\frac{1}{2}$ | D. | m=-$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com