
分析 (1)(2)(3)(4)(5)先化简,再分类计算即可;
(6)把原式变为1+(3-2)+(5-4)+…+(99-98),进一步计算得出答案即可.
解答 解:(1)原式=22-4-2+4
=20;
(2)原式=24+14-16-8
=14;
(3)原式=3$\frac{1}{2}$-$\frac{1}{2}$+$\frac{1}{3}$+2$\frac{2}{3}$
=6;
(4)原式=14+16+20
=50;
(5)原式=-1$\frac{1}{2}$-1$\frac{1}{4}$-2$\frac{1}{2}$+3$\frac{3}{4}$+1$\frac{1}{4}$
=-5$\frac{1}{4}$+5
=-$\frac{1}{4}$;
(6)原式=1+(3-2)+(5-4)+…+(99-98)
=50.
点评 此题考查了有理数的加减混合运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
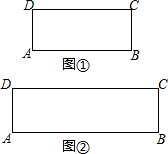 如果一个点与另外两个点能构成直角三角形,则称这个点为另外两个点的勾股点.例如:矩形ABCD中,点C与A、B两点可构成直角三角形ABC,则称点C为A、B两点的勾股点,同样,点D也是A、B两点的勾股点.
如果一个点与另外两个点能构成直角三角形,则称这个点为另外两个点的勾股点.例如:矩形ABCD中,点C与A、B两点可构成直角三角形ABC,则称点C为A、B两点的勾股点,同样,点D也是A、B两点的勾股点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+(b+c)=ab+c | B. | a2-[-(-a+b)]-a2-a+b=a2-a+b | ||
| C. | a+2(b-c)=a+2b-c | D. | a-(b+c-d)=a-b-c+d |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
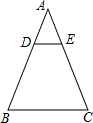 如图,若DE∥BC,则下列式子不成立的是( )
如图,若DE∥BC,则下列式子不成立的是( )| A. | $\frac{AD}{BD}$=$\frac{AE}{EC}$ | B. | $\frac{AD}{AB}$=$\frac{EC}{AC}$ | C. | $\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{DE}{BC}$ | D. | $\frac{BD}{AB}$=$\frac{EC}{AC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com