

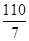 ,
,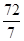 )
)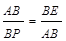 , 又∠ABE=∠PBA,
, 又∠ABE=∠PBA, ),并过点Q作QR⊥x轴于点R,由相似三角形性质、切割线定理、勾股定理、三角函数或直线解析式等可得多种解法.
),并过点Q作QR⊥x轴于点R,由相似三角形性质、切割线定理、勾股定理、三角函数或直线解析式等可得多种解法. 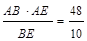 = 4.8(或
= 4.8(或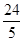 ).
).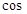 ∠BAQ2= 2+3.84=5.84,
∠BAQ2= 2+3.84=5.84,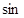 ∠BAQ2=2.88,
∠BAQ2=2.88,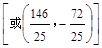 ………………………11分
………………………11分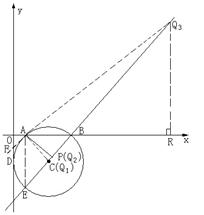
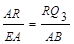 , ………………………13分
, ………………………13分 得t=
得t=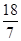 ,
,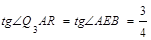 列得方程
列得方程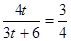 ; 或由AQ32 = Q3B·Q3E=Q3R2+AR2列得方程
; 或由AQ32 = Q3B·Q3E=Q3R2+AR2列得方程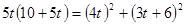 )等等〗
)等等〗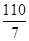 , Q3点的纵坐标为
, Q3点的纵坐标为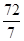 ,
,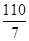 ,
,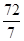 ) . …………14分
) . …………14分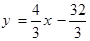 . ………………12分
. ………………12分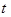 ,
,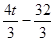 ),过点Q3作Q3R⊥x轴于点R,
),过点Q3作Q3R⊥x轴于点R, 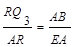 , 即
, 即 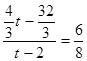 , ………………13分
, ………………13分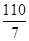 ,进而点Q3的纵坐标为
,进而点Q3的纵坐标为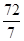 ,∴Q3(
,∴Q3(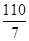 ,
,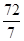 ). ………14分
). ………14分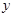 轴于F,
轴于F,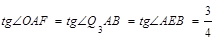 ,
,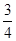 =
=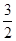 ,点F的坐标为(0,
,点F的坐标为(0,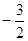 ),
),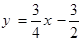 , …………………12分
, …………………12分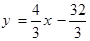 , ………………13分
, ………………13分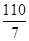 ,
,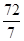 ). ……………………14分
). ……………………14分 ),并过点Q作QR⊥x轴于点R,由相似三角形性质、切割线定理、勾股定理、三角函数或直线解析式等可得多种解法.
),并过点Q作QR⊥x轴于点R,由相似三角形性质、切割线定理、勾股定理、三角函数或直线解析式等可得多种解法.

科目:初中数学 来源:不详 题型:单选题
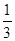 VA.过点B作平行与底面的平面截得一个小圆锥的侧面积为S1,原圆锥的侧面积为S,则下列判断中正确的是( )
VA.过点B作平行与底面的平面截得一个小圆锥的侧面积为S1,原圆锥的侧面积为S,则下列判断中正确的是( ) 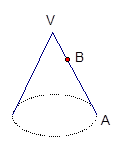
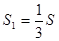 (B)
(B) 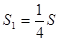 (C)
(C) 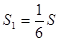 (D)
(D) 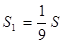
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
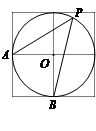
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com