
【题目】据统计,1980年世界人口的分布状况是:亚洲25.8亿人,欧洲7.5亿人,非洲4.6亿人,拉丁美洲3.5亿人,北美洲2.4亿人,大洋洲0.2亿人,全球合计44.0亿人.
(1)请制作一张统计图描述以上统计数据.
(2)请根据统计表格中的数据制作扇形统计图.
(3)从以上统计图、表中,你能得到哪些信息.
【答案】见解析
【解析】试题分析: ![]() 按要求列出表格即可.
按要求列出表格即可.
![]() 分别计算出各洲人数对应在扇形统计图中的圆心角,画图即可.
分别计算出各洲人数对应在扇形统计图中的圆心角,画图即可.
![]() 如亚洲人口最多等.
如亚洲人口最多等.
试题解析:(1)1980年世界人口分布统计表:
地域 | 亚洲 | 欧洲 | 非洲 | 拉丁美洲 | 北美洲 | 大洋洲 | 全球 |
人口(亿人) | 25.8 | 7.5 | 4.6 | 3.5 | 2.4 | 0.2 | 44.0 |
比例 | 58.6% | 17.0% | 10.4% | 8.0% | 5.5% | 0.5% | 100% |
(2)各部分对应的扇形所占的圆心角分别为:亚洲:360°×58.6%=210.96°.欧洲:360°×17.0%=61.2°.非洲:360°×10.4%=37.44°.拉丁美洲:360°×5.5%=19.8°.大洋洲:360°×0.5%=1.8°.扇形统计图如答图所示.
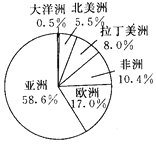
(3)学生可结合统计图表.表述自己获得的信息.合理即可.如亚洲人口最多.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y与x的部分取值满足下表:
![]()
(1)试猜想y与x的函数关系可能是你们学过的哪类函数,并写出这个函数的解析式.(不要求写x的取值范围)
(2)简要叙述该函数的性质.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m=_____.
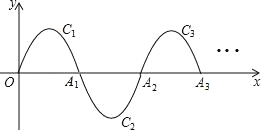
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为洪涛同学的小测卷(每小题25分,共100分),他的得分应是______分.
姓名 洪涛 得分?
填空
①2的相反数是 -2 ;
②倒数等于它本身的数是1和-1;
③-1的绝对值是 1 ;
④2的立方是 6 .
查看答案和解析>>
科目:初中数学 来源: 题型:
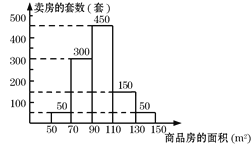
【题目】从某市近期卖出的不同面积的商 品房中随机抽取1000套进行统计,并根据结果绘出如图所示的统计图,请结合图中的信息,解析下列问题:
(1)卖出面积为110~130平方米的商品房 有___套,并在右图中补全统计图.
(2)从图中可知,卖出最多的商品房约占全部卖出的商品房的___%.

(3)假如你是房地产开发商,根据以上提供的信息,你会多建住房面积在什么范围内的住房?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,∠GEF=90°.
(1)若∠AGE=50°,求∠DFE的度数;
(2)若AG=2,DF=3,求GF的长;
(3)拓展研究:
如图2,在四边形ABCD中,∠A=105°,∠D=120°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=3,DF=2![]() ,∠GEF=90°,求GF的长.
,∠GEF=90°,求GF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com