
操作:小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的纸片进行如下设计:




说明:
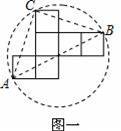
方案一:图形中的圆过点A、B、C;
方案二:直角三角形的两直角边与展开图左下角的正方形边重合,斜边经过两个正方形的顶点
纸片利用率=
 ×100%
×100%
发现:
(1)方案一中的点A、B恰好为该圆一直径的两个端点.你认为小明的这个发现是否正确,请说明理由.
(2)小明通过计算,发现方案一中纸片的利用率仅约为38.2%.请帮忙计算方案二的利用率,并写出求解过程.
探究:
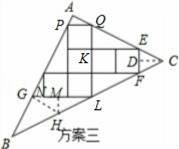
(3)小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.
说明:方案三中的每条边均过其中两个正方形的顶点.
【考点】相似三角形的判定与性质;几何体的展开图;勾股定理;圆周角定理.
【专题】几何综合题;压轴题;数形结合.
【分析】(1)连接AC、BC、AB,由AC=BC=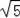
 ,AB=
,AB=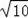
 ,根据勾股定理的逆定理,即可求得∠BAC=90°,又由90°的圆周角所对的弦是直径,则可证得AB为该圆的直径;
,根据勾股定理的逆定理,即可求得∠BAC=90°,又由90°的圆周角所对的弦是直径,则可证得AB为该圆的直径;
(2)首先证得△ADE≌△EHF与△ADE∽△ACB,即可求得AD与BC的长,求得△ABC的面积,即可求得该方案纸片利用率;
(3)利用方案(2)的方法,分析求解即可求得答案.
【解答】解:发现:(1)小明的这个发现正确.
理由:
解法一:如图一:连接AC、BC、AB,
∵AC=BC=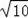
 ,AB=2
,AB=2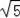

∴AC2+BC2=AB2,
∴∠BCA=90°,
∴AB为该圆的直径.
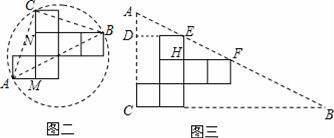
解法二:如图二:连接AC、BC、AB.
易证△AMC≌△BNC,
∴∠ACM=∠CBN.
又∵∠BCN+∠CBN=90°,
∴∠BCN+∠ACM=90°,
即∠BCA=90°,
∴AB为该圆的直径.


(2)如图三:∵DE=FH,DE∥FH,
∴∠AED=∠EFH,
∵∠ADE=∠EHF=90°,
∴△ADE≌△EHF(ASA),
∴AD=EH=1.
∵DE∥BC,
∴△ADE∽△ACB,
∴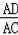
 =
=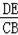
 ,
,
∴
 =
=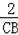
 ,
,
∴BC=8,
∴S△ACB=16.
∴该方案纸片利用率=
 ×100%=
×100%=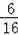
 ×100%=37.5%;
×100%=37.5%;
探究:(3)过点C作CD⊥EF于D,过点G作GH∥AC,交BC于点H,
设AP=a,
∵PQ∥EK,
易得△APQ∽△KQE,△CEF是等腰三角形,△GHL是等腰三角形,
∴AP:AQ=QK:EK=1:2,
∴AQ=2a,PQ=
 a,
a,
∴EQ=5a,
∵EC:ED=QE:QK,
∴EC=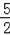
 a,
a,
则PG=5a+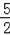
 a=
a=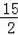
 a,GL=
a,GL=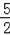

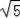
 a,
a,
∴GH=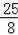
 a,
a,
∵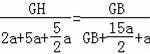
 ,
,
解得:GB=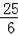
 a,
a,
∴AB=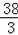
 a,AC=
a,AC=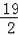
 a,
a,
∴S△ABC=
 ×AB×AC=
×AB×AC=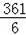
 a2,
a2,
S展开图面积=6×5a2=30a2,
∴该方案纸片利用率=
 ×100%=
×100%=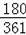
 ×100%=49.86%.
×100%=49.86%.

【点评】此题考查了圆周角的性质,相似三角形与全等三角形的判定与性质,勾股定理的逆定理等知识.此题综合性很强,难度较大,解题时要注意数形结合思想的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).


查看答案和解析>>
科目:初中数学 来源: 题型:
大明因急事在运行中的自动扶梯上行走去二楼(如图1),图2中线段OA、OB分别表示大明在运行中的自动扶梯上行走去二楼和静止站在运行中的自动扶梯上去二楼时,距自动扶梯起点的距离与时间之间的关系.下面四个图中,虚线OC能大致表示大明在停止运行(即静止)的自动扶梯上行走去二楼时,距自动扶梯起点的距离与时间关系的是( )


A.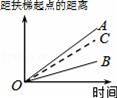
 B.
B.

C.
 D.
D.

查看答案和解析>>
科目:初中数学 来源: 题型:
房山某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下的两个统计图.请根据下面两个不完整的统计图回答以下问题:
(1)这次抽样调查中,共调查了 500 名学生;
(2)补全两幅统计图;
(3)根据抽样调查的结果,估算该校1000名学生中大约有多少人选择“小组合作学习”?


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com