
��ɽij��ѧ�ĸ�ѧ����ѧϰģʽ���䡰��ʦҪѧ��ѧϰ��Ϊ��ѧ������ѧϰ����������ѧ������ѧϰ��������С����С��ͬѧ�͡���ϲ������ѧϰ��ʽ�����������������Χ��һЩͬѧ�������ռ��������ݻ��������µ�����ͳ��ͼ�����������������������ͳ��ͼ�ش��������⣺
��1����γ��������У�����������500����ѧ����
��2����ȫ����ͳ��ͼ��
��3�����ݳ�������Ľ���������У1000��ѧ���д�Լ�ж�����ѡ��С�����ѧϰ����


�����㡿����ͳ��ͼ���������������壻����ͳ��ͼ��
����������1�����ݸ�����ѧ����ʦ�㲦����������ռ�İٷֱ�������������ɣ�
��2����С�����ѧϰ�����������������ó�С�����ѧϰ��ռ�İٷֱȣ�����������ȥ����ѧϰ��ʽ�����������ʦ���ڵ��������ٳ����������������ʦ���ڵ�������ռ�İٷֱȣ��Ӷ���ȫͳ��ͼ��
��3���ø�У�����������ԡ�С�����ѧϰ����ռ�İٷֱȼ��ɵó��𰸣�
����𡿽⣺��1����γ��������У��������ѧ�����ǣ�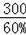
 =500��������
=500��������
�ʴ�Ϊ��500��
��2��С�����ѧϰ��ռ�İٷֱ��ǣ�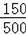
 ��100%=30%��
��100%=30%��
��ʦ���ڵ������ǣ�500��300��150=50���ˣ���
��ʦ������ռ�İٷֱ��ǣ�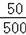
 ��100%=10%��
��100%=10%��
��ͼ���£�
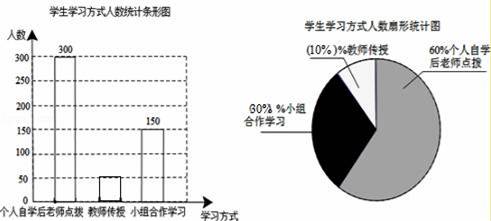

��3����������ã�
1000��30%=300���ˣ���
�𣺸�У1000��ѧ���д�Լ��300��ѡ��С�����ѧϰ����
�����������⿼���������ͳ��ͼ������ͳ��ͼ���ۺ����ã�����ͳ��ͼ���Ӳ�ͬ��ͳ��ͼ�еõ���Ҫ����Ϣ�ǽ������Ĺؼ�������ͳ��ͼ������ر�ʾ��ÿ����Ŀ�����ݣ�����ͳ��ͼֱ�ӷ�ӳ����ռ����İٷֱȴ�С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
������С���������ⳤΪ1cm��������ֽ�У���ѡ��һЩ������ֽƬ����������ƣ�




˵����
����һ��ͼ���е�Բ����A��B��C��
��������ֱ�������ε���ֱ�DZ���չ��ͼ���½ǵ������α��غϣ�б�߾������������εĶ���
ֽƬ������=
 ��100%
��100%
���֣�
��1������һ�еĵ�A��Bǡ��Ϊ��Բһֱ���������˵㣮����ΪС������������Ƿ���ȷ����˵�����ɣ�
��2��С��ͨ�����㣬���ַ���һ��ֽƬ�������ʽ�ԼΪ38.2%�����æ���㷽�����������ʣ���д�������̣�
̽����
��3��С���о��������������������ʾ�ƫ�ͣ��ֽ������µ���ƣ�������������ֱ��д���������������ʣ�
˵�����������е�ÿ���߾����������������εĶ��㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
������x�ķ���x2+3x+a=0��һ����Ϊ��1������һ����Ϊ��������
A����2 B��2 C��4 D����3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��ABΪ��Oֱ����C��DΪ��O�ϲ�ͬ��A��B�����㣬��ABD=2��BAC������C��CE��DB������ΪE��ֱ��AB��CE�ཻ��F�㣮
��1����֤��CFΪ��O�����ߣ�
��2������O�İ뾶Ϊ
 cm����BD�ij�Ϊ3cm����CF�ij���
cm����BD�ij�Ϊ3cm����CF�ij���
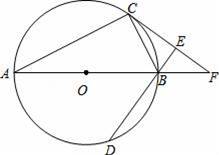

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ���ı���ABCD�ڽ��ڡ�O��AD��BC���ӳ����ཻ�ڵ�E��AB��DC���ӳ����ཻ�ڵ�F������E+��F=80�㣬���A=�����㣮


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��ʾ����Ϊ50cm�ľ���ͼ����10��ȫ�ȵij�����ƴ�ɣ�����һ��С�����ε����Ϊ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���¸�ʽ������ȷ���ǣ�������
A����y+x������y+x��=y2��x2 B����
 =��2
=��2
C������2a2��3=��8a6 D��x6��x3=x2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com