
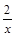 于点D,过D作两坐标轴的垂线DC、DE,连接OD.
于点D,过D作两坐标轴的垂线DC、DE,连接OD.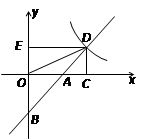
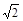 CD,BD=
CD,BD=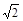 DE,则可得AD·BD=2CD·DE=2×2=4为定值;(3)y=x-1
DE,则可得AD·BD=2CD·DE=2×2=4为定值;(3)y=x-1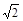 CD,BD=
CD,BD=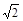 DE,则可得AD·BD=2CD·DE=2×2=4为定值;
DE,则可得AD·BD=2CD·DE=2×2=4为定值;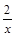 上即可求得a的值,从而可以求得结果.
上即可求得a的值,从而可以求得结果.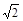 CD,BD=
CD,BD=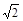 DE
DE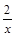 上,
上,

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源:不详 题型:解答题
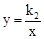 的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线。
的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线。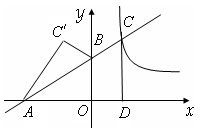
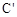 是点C关于y轴的对称点,请求出△
是点C关于y轴的对称点,请求出△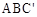 的面积。
的面积。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
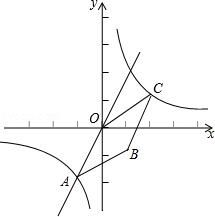
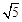 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
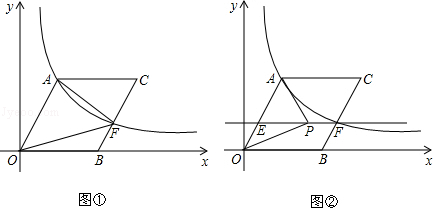
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
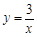 ,
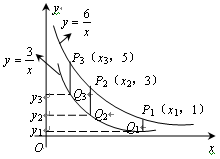
,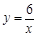 在第一象限内的图像如图所示,点
在第一象限内的图像如图所示,点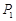 ,
,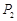 ,
,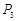 ,…,
,…,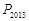 在函数
在函数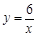 的图像上,它们的横坐标分别是
的图像上,它们的横坐标分别是 ,
,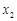 ,
,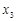 ,…,
,…,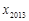 ,纵坐标分别是1,3,5,…,共2013个连续奇数,过点
,纵坐标分别是1,3,5,…,共2013个连续奇数,过点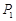 ,
,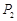 ,
,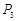 ,…,
,…,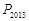 分别作y轴的平行线,与函数
分别作y轴的平行线,与函数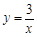 的图像交点依次是
的图像交点依次是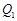 (
( ,
,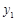 ),
), (
(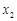 ,
,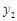 ),
),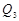 (
(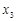 ,
,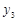 ),…,
),…,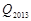 (
(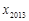 ,
,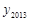 ),则
),则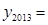 .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
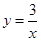 ,下列说法中错误的是( )
,下列说法中错误的是( )| A.它的图象分布在一、三象限 |
| B.它的图象过点(-1,-3) |
| C.当x>0时,y的值随x的增大两增大 |
| D.当x<0时,y的值随x的增大而减小 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
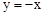 与函数
与函数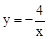 的图象相交于A,B两点,过A,B两点分别作y轴的垂线,垂足分别为点C,D.则四边形ACBD的面积为
的图象相交于A,B两点,过A,B两点分别作y轴的垂线,垂足分别为点C,D.则四边形ACBD的面积为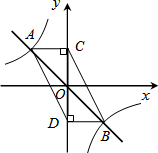
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com