
.已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.
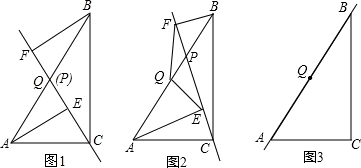
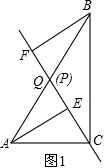
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是__________,QE与QF的数量关系式__________;
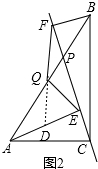
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
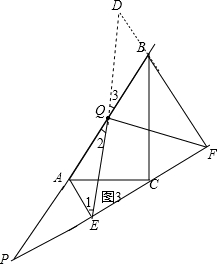
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.
【考点】全等三角形的判定与性质;直角三角形斜边上的中线.
【专题】压轴题.
【分析】(1)证△BFQ≌△AEQ即可;
(2)证△FBQ≌△DAQ,推出QF=QD,根据直角三角形斜边上中线性质求出即可;
(3 )证△AEQ≌△BDQ,推出DQ=QE,根据直角三角形斜边上中线性质求出即可.
)证△AEQ≌△BDQ,推出DQ=QE,根据直角三角形斜边上中线性质求出即可.
【解答】解:(1)AE∥BF,QE=QF,
理由是:如图1,∵Q为AB中点,
∴AQ=BQ,
∵BF⊥CP,AE⊥CP,
∴BF∥AE,∠BFQ=∠AEQ=90°,
在△BFQ和△AEQ中
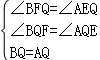
∴△BFQ≌△AEQ(AAS),
∴QE=QF,
故答案为:AE∥BF;QE=QF.
(2)QE=QF,
证明:如图2,延长FQ交AE于D,
∵Q为AB中点,
∴AQ=BQ,
∵BF⊥CP,AE⊥CP,
∴BF∥AE,
∴∠QAD=∠FBQ,
在△FBQ和△DAQ中
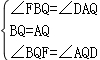
∴△FBQ≌△DAQ(ASA),
∴QF=QD,
∵AE⊥CP,
∴EQ是直角三角形DEF斜边上的中线,
∴QE=QF=QD,
即QE=QF.
(3)(2)中的结论仍然成立,
证明:如图3,
延长EQ、FB交于D,
∵Q为AB中点,
∴AQ=BQ,
∵BF⊥CP,AE⊥CP,
∴BF∥AE,
∴∠1=∠D,
在△AQE和△BQD中,
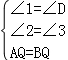 ,
,
∴△AQE≌△BQD(AAS),
∴QE=QD,
∵BF⊥CP,
∴FQ是斜边DE上的中线,
∴QE=QF.
【点评】本题考查了全等三角形的性质和判定,直角三角形斜边上中线性质的应用,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的性质是:全等三角形的对应边相等,对应角相等.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,F为BC的中点,DE=5,BC=8,则△DEF的周长是( )
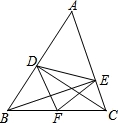
A.21 B.18 C.13 D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
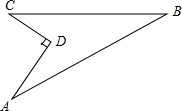
如图,某住宅小区在施工过程中留下了一块空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
.如图,校园有两条路OA、OB,在交叉路口附近有两块宣传牌C、D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你帮助画出灯柱的位置P,简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )

A.1对 B.2对 C.3对 D.4对
查看答案和解析>>
科目:初中数学 来源: 题型:
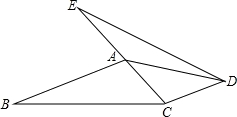
已知:如图,点E、A、C在同一条直线上,AB∥CD,AB=CE,∠B=∠E.
(1)求证:△ABC≌△CED;
(2)若∠B=25°,∠ACB=45°,求∠ADE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com