
【题目】如图,已知等边![]() 的边长为8,
的边长为8,![]() 是中线
是中线![]() 上一点,以
上一点,以![]() 为一边在
为一边在![]() 下方作等边
下方作等边![]() ,连接
,连接![]() 并延长至点
并延长至点![]() 为
为![]() 上一点,且
上一点,且![]() ,则
,则![]() 的长为_________.
的长为_________.
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 的解析式为
的解析式为![]() ,点
,点![]() 的坐标分别为(1,0),(0,2),直线
的坐标分别为(1,0),(0,2),直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
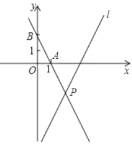
(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 在第一象限的直线
在第一象限的直线![]() 上,连接
上,连接![]() ,且
,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() 的图象经过点(﹣1,﹣2
的图象经过点(﹣1,﹣2![]() ),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,当
),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,当![]() 时,则点C的坐标为______.
时,则点C的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蔬菜基地种植了娃娃菜和油菜两种蔬菜共![]() 亩,设种植娃娃菜
亩,设种植娃娃菜![]() 亩,总收益为
亩,总收益为![]() 万元,有关数据见下表:
万元,有关数据见下表:
成本(单位:万元/亩) | 销售额(单位:万元/亩) | |
娃娃菜 | 2.4 | 3 |
油菜 | 2 | 2.5 |
(1)求![]() 关于
关于![]() 的函数关系式(收益 = 销售额 – 成本);
的函数关系式(收益 = 销售额 – 成本);
(2)若计划投入的总成本不超过![]() 万元,要使获得的总收益最大,基地应种植娃娃菜和油菜各多少亩?
万元,要使获得的总收益最大,基地应种植娃娃菜和油菜各多少亩?
(3)已知娃娃菜每亩地需要化肥![]() kg,油菜每亩地需要化肥
kg,油菜每亩地需要化肥![]() kg,根据(2)中的种植亩数,基地计划运送所需全部化肥,为了提高效率,实际每次运送化肥的总量是原计划的
kg,根据(2)中的种植亩数,基地计划运送所需全部化肥,为了提高效率,实际每次运送化肥的总量是原计划的![]() 倍,结果运送完全部化肥的次数比原计划少
倍,结果运送完全部化肥的次数比原计划少![]() 次,求基地原计划每次运送多少化肥.
次,求基地原计划每次运送多少化肥.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:矩形![]() ,点
,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() ,
,![]() ,且
,且![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() .
.
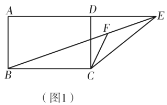
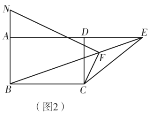
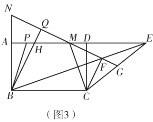
(1)如图1,求![]() 的大小;
的大小;
(2)如图2,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]() ,且
,且![]() .延长
.延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 的周长与
的周长与![]() 的周长的差为2,求
的周长的差为2,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D,E分别是不等边△ABC(即AB,BC,AC互不相等)的边AB,AC的中点.点O是△ABC所在平面上的动点,连接OB,OC,点G,F分别是OB,OC的中点,顺次连接点D,G,F,E.
(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(直接写出答案,不需要说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某贮水塔在工作期间,每小时的进水量和出水量都是固定不变的.从凌晨4点到早8点只进水不出水,8点到12点既进水又出水,14点到次日凌晨只出水不进水.下图是某日水塔中贮水量y(立方米)与x(时)的函数图象.
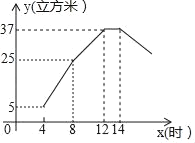
(1)求每小时的进水量;
(2)当8≤x≤12时,求y与x之间的函数关系式;
(3)从该日凌晨4点到次日凌晨,当水塔中的贮水量不小于28立方米时,直接写出x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com