
【题目】已知边长为2a的正方形ABCD,对角线AC、BD交于点Q,对于平面内的点P与正方形ABCD,给出如下定义:如果![]() ,则称点P为正方形ABCD的“关联点”.在平面直角坐标系xOy中,若A(﹣1,1),B(﹣1,﹣1),C(1,﹣1),D(1,1).
,则称点P为正方形ABCD的“关联点”.在平面直角坐标系xOy中,若A(﹣1,1),B(﹣1,﹣1),C(1,﹣1),D(1,1).
(1)在![]() ,
,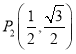 ,
,![]() 中,正方形ABCD的“关联点”有_____;
中,正方形ABCD的“关联点”有_____;
(2)已知点E的横坐标是m,若点E在直线![]() 上,并且E是正方形ABCD的“关联点”,求m的取值范围;
上,并且E是正方形ABCD的“关联点”,求m的取值范围;
(3)若将正方形ABCD沿x轴平移,设该正方形对角线交点Q的横坐标是n,直线![]() 与x轴、y轴分别相交于M、N两点.如果线段MN上的每一个点都是正方形ABCD的“关联点”,求n的取值范围.
与x轴、y轴分别相交于M、N两点.如果线段MN上的每一个点都是正方形ABCD的“关联点”,求n的取值范围.
【答案】(1)正方形ABCD的“关联点”为P2,P3;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)正方形ABCD的“关联点”中正方形的内切圆和外切圆之间(包括两个圆上的点),由此画出图形即可判断;
(2)因为E是正方形ABCD的“关联点”,所以E在正方形ABCD的内切圆和外接圆之间(包括两个圆上的点),因为E在直线![]() 上,推出点E在线段FG上,求出点F、G的横坐标,再根据对称性即可解决问题;
上,推出点E在线段FG上,求出点F、G的横坐标,再根据对称性即可解决问题;
(3)因为线段MN上的每一个点都是正方形ABCD的“关联点”,分两种情形:①如图3中,MN与小⊙Q相切于点F,求出此时点Q的横坐标;②M如图4中,落在大⊙Q上,求出点Q的横坐标即可解决问题;
(1)由题意正方形ABCD的“关联点”中正方形的内切圆和外切圆之间(包括两个圆上的点),
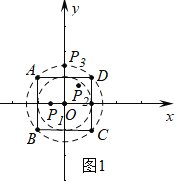
观察图象可知:正方形ABCD的“关联点”为P2,P3;
(2)作正方形ABCD的内切圆和外接圆,
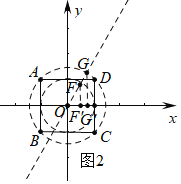
∴OF=1,![]() ,.
,.
∵E是正方形ABCD的“关联点”,
∴E在正方形ABCD的内切圆和外接圆之间(包括两个圆上的点),
∵点E在直线![]() 上,
上,
∴点E在线段FG上.
分别作FF’⊥x轴,GG’⊥x轴,
∵OF=1,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
根据对称性,可以得出![]() .
.
∴![]() 或
或![]() .
.
(3)∵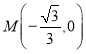 、N(0,1),
、N(0,1),
∴![]() ,ON=1.
,ON=1.
∴∠OMN=60°.
∵线段MN上的每一个点都是正方形ABCD
的“关联点”,
①MN与小⊙Q相切于点F,如图3中,

∵QF=1,∠OMN=60°,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴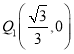 .
.
②M落在大⊙Q上,如图4中,
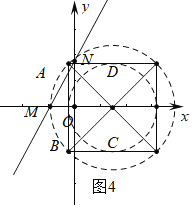
∵![]() ,
,![]() ,
,
∴![]() .
.
∴ .
.
综上:![]() .
.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
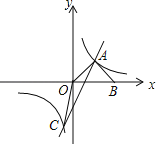
【题目】如图,在平面直角坐标系中,直线y1=2x﹣2与双曲线y2=![]() 交于A、C两点,AB⊥OA交x轴于点B,且AB=OA.
交于A、C两点,AB⊥OA交x轴于点B,且AB=OA.
(1)求双曲线的解析式;
(2)连接OC,求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
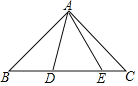
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°
(1)若BD=2,CE=4,则DE=_____.
(2)若∠AEB=75°,则线段BD与CE的数量关系是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年2月,美国宇航局(NASA)的卫星监测数据显示地球正在变绿,分析发现是中国和印度的行动主导了地球变绿.尽管中国和印度的土地面积加起来只占全球的9%,但过去20年间地球三分之一的新增植被是两国贡献的,面积相当于一个亚马逊雨林.已知亚马逊雨林的面积为6560000km![]() ,则过去20年间地球新增植被的面积约为( )
,则过去20年间地球新增植被的面积约为( )
A.6.56×10![]() km
km![]() B.6.56×10
B.6.56×10![]() km
km![]() C.2×10
C.2×10![]() km
km![]() D.2×10
D.2×10![]() km
km![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系 xOy 中,直线 l:![]() 与 x 轴交于点 A(-2,0),与 y 轴交于点 B.双曲线
与 x 轴交于点 A(-2,0),与 y 轴交于点 B.双曲线![]() 与直线 l 交于 P,Q 两点,其中点 P 的纵坐标大于点 Q 的纵坐标.
与直线 l 交于 P,Q 两点,其中点 P 的纵坐标大于点 Q 的纵坐标.
(1)求点 B 的坐标;
(2)当点 P 的横坐标为 2 时,求 k 的值;
(3)连接 PO,记△POB 的面积为 S,若![]() ,直接写出 k 的取值范围.
,直接写出 k 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,a),B(﹣1,2)是一次函数y1=kx+b与反比例函数y2=![]() (m<0)图象的两个交点,AC⊥x轴于C.
(m<0)图象的两个交点,AC⊥x轴于C.

(1)求出k,b及m的值.
(2)根据图象直接回答:在第二象限内,当y1>y2时,x的取值范围是 ________.
(3)若P是线段AB上的一点,连接PC,若△PCA的面积等于![]() ,求点P坐标.
,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
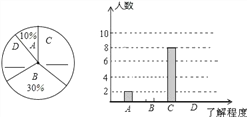
【题目】2013年5月31日是第26个“世界无烟日”,校学生会书记小明同学就“戒烟方式”的了解程度对本校九年级学生进行了一次随机问卷调查,如图是他采集数据后绘制的两幅不完整的统计图(A:了解较多,B:不了解,C:了解一点,D:非常了解).请你根据图中提供的信息解答以下问题:
(1)在扇形统计图中的横线上填写缺失的数据,并把条形统计图补充完整.
(2)2013年该初中九年级共有学生400人,按此调查,可以估计2013年该初中九年级学生中对戒烟方式“了解较多”以上的学生约有多少人?
(3)在问卷调查中,选择“A”的是1名男生,1名女生,选择“D”的有4人且有2男2女.校学生会要从选择“A、D”的问卷中,分别抽一名学生参加活动,请你用列表法或树状图求出恰好是一名男生一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,BC=2AB,E,F分别是BC,AD的中点,AE,BF交于点O,连接EF,OC.
(1)求证:四边形ABEF是菱形;(2)若BC=8,∠ABC=60°,求OC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)模型探究:如图1,![]() 、
、![]() 、
、![]() 分别为
分别为![]() 三边
三边![]() 、
、![]() 、
、![]() 上的点,且
上的点,且![]() ,
,![]() 与
与![]() 相似吗?请说明理由.
相似吗?请说明理由.

(2)模型应用:![]() 为等边三角形,其边长为
为等边三角形,其边长为![]() ,
,![]() 为边
为边![]() 上一点,
上一点,![]() 为射线
为射线![]() 上一点,将
上一点,将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在射线
落在射线![]() 上的点
上的点![]() 处,且
处,且![]() .
.
①如图2,当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 的值;
的值;

②如图3,当点![]() 落在线段
落在线段![]() 的延长线上时,求
的延长线上时,求![]() 与
与![]() 的周长之比.
的周长之比.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com