
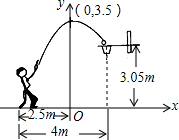
 如图,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
如图,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.分析 (1)设抛物线的表达式为y=ax2+3.5,依题意可知图象经过的坐标,由此可得a的值.
(2)设球出手时,他跳离地面的高度为hm,则可得h+1.95=-0.2×(-2.5)2+3.5.
解答 解:(1)∵当球运行的水平距离为2.5米时,达到最大高度3.5米,
∴抛物线的顶点坐标为(0,3.5),
∴设抛物线的表达式为y=ax2+3.5.
由图知图象过以下点:(1.5,3.05).
∴2.25a+3.5=3.05,
解得:a=-0.2,
∴抛物线的表达式为y=-0.2x2+3.5.
(2)设球出手时,他跳离地面的高度为hm,
因为(1)中求得y=-0.2x2+3.5,
则球出手时,球的高度为h+1.7+0.25=(h+2.05)m,
∴h+1.95=-0.2×(-2.5)2+3.5,
∴h=0.3.
答:球出手时,他跳离地面的高度为0.3m.
点评 本题考查了二次函数的应用,解题的关键是从实际问题中抽象出二次函数模型,体现了数学建模的数学思想,难度不大,能够结合题意利用二次函数不同的表达形式求得解析式是解答本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠C=90°,tanA=$\frac{2}{5}$,D为AC上一点,∠BDC=60°,DC=2$\sqrt{3}$,求AD的长.
如图,在△ABC中,∠C=90°,tanA=$\frac{2}{5}$,D为AC上一点,∠BDC=60°,DC=2$\sqrt{3}$,求AD的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com