
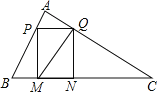
【题目】定义:若一个三角形一条边上的高长为这条边长的一半,则称该三角形为这条边上的“半高”三角形,这条高称为这条边上的“半高”,如图,△ABC是BC边上的“半高”三角形.点P在边AB上,PQ∥BC交AC于点Q,PM⊥BC于点M,QN⊥BC于点N,连接MQ.
(1)请证明△APQ为PQ边上的“半高”三角形.
(2)请探究BM,PM,CN之间的等量关系,并说明理由;
(3)若△ABC的面积等于16,求MQ的最小值
【答案】(1)见解析;(2)2PM=BM+CN,理由见解析;(3)![]() .
.
【解析】
(1)根据平行相似,证明△APQ∽△ABC,利用相似三角形对应边的比等于对应高的比:![]() ,由“半高”三角形的定义可结论;
,由“半高”三角形的定义可结论;
(2)证明四边形PMNQ是矩形,得PQ=MN,PM=KR,代入AR=![]() BC,可得结论;
BC,可得结论;
(3)先根据△ABC的面积等于16,计算BC和AR的长,设MN=x,则BM+CN=8﹣x,PM=QN=![]() (8﹣x),根据勾股定理表示MQ,配方可得最小值.
(8﹣x),根据勾股定理表示MQ,配方可得最小值.
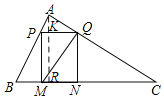
(1)证明:如图,过A作AR⊥BC于R,交PQ于K,
∵△ABC是BC边上的“半高”三角形,
∴AR=![]() BC,
BC,
∵PQ∥BC,
∴△APQ∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴AK=![]() PQ,
PQ,
∴△APQ为PQ边上的“半高”三角形.
(2)解:2PM=BM+CN,理由是:
∵PM⊥BC,QN⊥BC,
∴∠PMN=∠MNQ=∠MPQ=90°,
∴四边形PMNQ是矩形,
∴PQ=MN,PM=KR,
∵AK=![]() PQ,AR=
PQ,AR=![]() BC,
BC,
∴AK+RK=![]() (BM+MN+CN),
(BM+MN+CN),
![]() PQ+PM=
PQ+PM=![]() BM+
BM+![]() MN+
MN+![]() CN,
CN,
∴2PM=BM+CN;
(3)解:∵△ABC的面积等于16,
∴![]() =16,
=16,
∵AR=![]() BC,
BC,
![]() =16,
=16,
BC=8,AR=4,
设MN=x,则BM+CN=8﹣x,PM=QN=![]() (8﹣x),
(8﹣x),
∵MQ=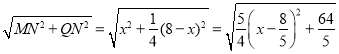 ,
,
∴当x=![]() 时,MQ有最小值是
时,MQ有最小值是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
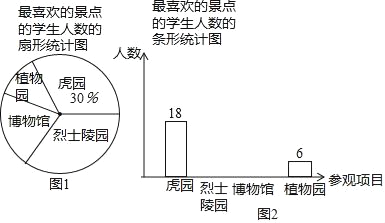
【题目】某校在一次社会实践活动中,组织学生参观了虎园、烈士陵园、博物馆和植物园,为了解本次社会实践活动的效果,学校随机抽取了部分学生,对“最喜欢的景点”进行了问卷调查,并根据统计结果绘制了如下不完整的统计图.其中最喜欢烈士陵园的学生人数与最喜欢博物馆的学生人数之比为2:1,请结合统计图解答下列问题:
(1)本次活动抽查了 名学生;
(2)请补全条形统计图;
(3)在扇形统计图中,最喜欢植物园的学生人数所对应扇形的圆心角是 度;
(4)该校此次参加社会实践活动的学生有720人,请求出最喜欢烈士陵园的人数约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现
如图1,在有一个“凹角∠A1A2A3”n边形A1A2A3A4……An中(n为大于3的整数),∠A1A2A3=∠A1+∠A3+∠A4+∠A5+∠A6+……+∠An﹣(n﹣4)×180°.
验证
(1)如图2,在有一个“凹角∠ABC”的四边形ABCD中,证明:∠ABC=∠A+∠C+∠D.
(2)证明3,在有一个“凹角∠ABC”的六边形ABCDEF中,证明;∠ABC=∠A+∠C+∠D+∠E+∠F﹣360°.
延伸
(3)如图4,在有两个连续“凹角A1A2A3和∠A2A3A4”的四边形A1A2A3A4……An中(n为大于4的整数),∠A1A2A3+∠A2A3A4=∠A1+∠A4+∠A5+∠A6……+∠An﹣(n﹣ )×180°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任意抛掷一枚质地均匀的正方体骰子2次,骰子的6个面上分别刻有1到6的点数,记第一次掷得面朝上的点数为横坐标,第二次掷得面朝上的点数为纵坐标,这样组成的点的坐标恰好在正比例函数y=x上的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
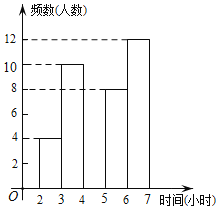
【题目】某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) | 频数(人数) | 频率 |
2≤t<3 | 4 | 0.1 |
3≤t<4 | 10 | 0.25 |
4≤t<5 | a | 0.15 |
5≤t<6 | 8 | b |
6≤t<7 | 12 | 0.3 |
合计 | 40 | 1 |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
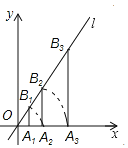
【题目】如图,点A1的坐标为(2,0),过点A1作x轴的垂线交直线l:y=![]() x于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2,则点A2的坐标为_____;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则
x于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2,则点A2的坐标为_____;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则![]() 的长是_____.
的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
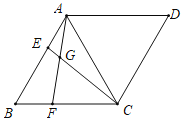
【题目】已知:如图,在菱形ABCD中,AB=AC,点E、F分别在边AB、BC上,且AE=BF,CE与AF相交于点G.
(1)求证:∠FGC=∠B;
(2)延长CE与DA的延长线交于点H,求证:BECH=AFAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
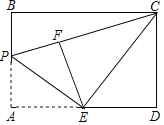
【题目】如图,在矩形ABCD中,AB=4,AD=6,点E为AD的中点,点P为线段AB上一个动点,连接EP,将△APE沿EP折叠得到△EPF,连接CE,CF,当△ECF为直角三角形时,AP的长为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com