
【题目】如图:已知△ABC为直角三角形,分别以直角边AC、BC为直径作半圆AmC和BnC,以AB为直径作半圆ACB,记两个月牙形阴影部分的面积之和为S1,△ABC的面积为S2,则S1与S2的大小关系为( )

A. S1>S2 B. S1<S2 C. S1=S2 D. 不能确定
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,四个全等的直角三角形纸片既可以拼成(内角不是直角)的菱形ABCD,也可以拼成正方形EFGH,则菱形ABCD面积和正方形EFGH面积之比为( ) 
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线y=﹣x﹣4分别交x、y轴于A、C两点,抛物线y=ax2+bx(a>0)经过A、O两点,且顶点B的纵坐标为﹣2 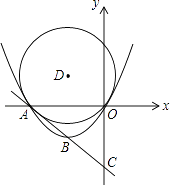
(1)判断点B是否在直线AC上,并求该抛物线的函数关系式;
(2)以点B关于x轴的对称点D为圆心,以OD为半径作⊙D,试判断直线AC与⊙D的位置关系,并说明理由;
(3)若E为⊙D的优弧AO上一动点(不与A、O重合),连结AE、OE,问在抛物线上是否存在点P,使∠POA:∠AEO=2:3?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是切⊙O于A的切线,BC交⊙O于点D,E是劣弧 ![]() 的中点,连接AE交BC于点F,若cosC=
的中点,连接AE交BC于点F,若cosC= ![]() ,AC=6,则BF的长为 .
,AC=6,则BF的长为 . 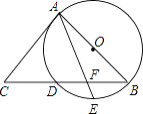
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知ΔABC的三边长为a、b、c,下列条件能够说明ΔABC是直角三角形的是( )
A. a:b:c=5:12:15 B. 3a=4b=5c C. a:b:c=1:2:![]() D. a=b=
D. a=b=![]() c
c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自开展“学生每天锻炼1小时”活动后,我市某中学根据学校实际情况,决定开设A:毽子,B:篮球,C:跑步,D:跳绳四种运动项目.为了了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图统计图.请结合图中信息解答下列问题:
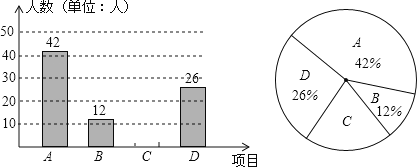
(1)该校本次调查中,共调查了多少名学生?
(2)请将两个统计图补充完整;
(3)在本次调查的学生中随机抽取1人,他喜欢“跑步”的概率有多大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具厂熟练工人工资为:每月底薪700元,加奖励工资按件计算,一个月工作日为25天,每天工作8小时,加工1件A种玩具计酬10元,加工1件B种玩具计酬8元.在工作中发现一名熟练工人加工1件A种玩具和2件B种玩具需4小时,加工3件A种玩具和1件B种玩具需7小时.(工人月工资=底薪+计件工资)
(1)求熟练工人每加工一件A种玩具和一件B种玩具,分别需要多少时间?
(2)深圳市规定最低工资标准为每月2030元,但玩具厂规定:“每名工人每月必须加工A、B两种工具,且加工A种玩具数量不少于B种玩具的一半”.若设一名熟练工人每月加工A种玩具a件,工资总额为w元,请你运用所学知识判断该公司在执行规定后是否违背了深圳市最低工资标准?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳池有水4000m3 , 先放水清洗池子.同时,工作人员记录放水的时间x(单位:分钟)与池内水量y(单位:m3) 的对应变化的情况,如下表:
时间x(分钟) | … | 10 | 20 | 30 | 40 | … |
水量y(m3) | … | 3750 | 3500 | 3250 | 3000 | … |
(1)根据上表提供的信息,当放水到第80分钟时,池内有水多少m3?
(2)请你用函数解析式表示y与x的关系,并写出自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com