
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпl1ЃКy=Љx2+bx+3НЛxжсгкЕуAЁЂBЃЌЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌНЛyжсгкЕуCЃЌЦфЖдГЦжсЮЊx=1ЃЌХзЮяЯпl2ОЙ§ЕуAЃЌгыxжсЕФСэвЛИіНЛЕуЮЊEЃЈ5ЃЌ0ЃЉЃЌНЛyжсгкЕуDЃЈ0ЃЌЉ5ЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпl2ЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉPЮЊжБЯпx=1ЩЯвЛЖЏЕуЃЌСЌНгPAЁЂPCЃЌЕБPA=PCЪБЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉMЮЊХзЮяЯпl2ЩЯвЛЖЏЕуЃЌЙ§ЕуMзїжБЯпMNЁЮyжсЃЈШчЭМ2ЫљЪОЃЉЃЌНЛХзЮяЯпl1гкЕуNЃЌЧѓЕуMздЕуAдЫЖЏжСЕуEЕФЙ§ГЬжаЃЌЯпЖЮMNГЄЖШЕФзюДѓжЕЃЎ
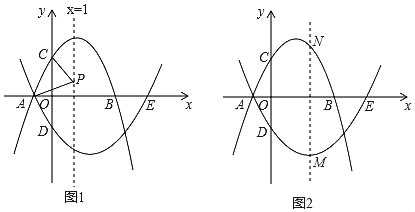
ЁОД№АИЁПЃЈ1ЃЉХзЮяЯпl2ЕФКЏЪ§БэДяЪНЃЛy=x2Љ4xЉ5ЃЛЃЈ2ЃЉPЕузјБъЮЊЃЈ1ЃЌ1ЃЉЃЛЃЈ3ЃЉдкЕуMздЕуAдЫЖЏжСЕуEЕФЙ§ГЬжаЃЌЯпЖЮMNГЄЖШЕФзюДѓжЕЮЊ12.5ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩХзЮяЯпl1ЕФЖдГЦжсЧѓГіbЕФжЕЃЌМДПЩЕУГіХзЮяЯпl1ЕФНтЮіЪНЃЌДгЖјЕУГіЕуAЁЂЕуBЕФзјБъЃЌгЩЕуBЁЂЕуEЁЂЕуDЕФзјБъЧѓГіХзЮяЯпl2ЕФНтЮіЪНМДПЩЃЛЃЈ2ЃЉзїCHЁЭPGНЛжБЯпPGгкЕуHЃЌЩшЕуPЕФзјБъЮЊЃЈ1ЃЌyЃЉЃЌЧѓГіЕуCЕФзјБъЃЌНјЖјЕУГіCH=1ЃЌPH=|3Љy |ЃЌPG=|y |ЃЌAG=2ЃЌгЩPA=PCПЩЕУPA2=PC2ЃЌгЩЙДЙЩЖЈРэЗжБ№НЋPA2ЁЂPC2гУCHЁЂPHЁЂPGЁЂAGБэЪОЃЌСаЗНГЬЧѓГіyЕФжЕМДПЩЃЛЃЈ3ЃЉЩшГіЕуMЕФзјБъЃЌЧѓГіСНИіХзЮяЯпНЛЕуЕФКсзјБъЗжБ№ЮЊЉ1ЃЌ4ЃЌЂйЕБЉ1ЃМxЁм4ЪБЃЌЕуMЮЛгкЕуNЕФЯТЗНЃЌБэЪОГіMNЕФГЄЖШЮЊЙигкxЕФЖўДЮКЏЪ§ЃЌдкxЕФЗЖЮЇФкЧѓЖўДЮКЏЪ§ЕФзюжЕЃЛЂкЕБ4ЃМxЁм5ЪБЃЌЕуMЮЛгкЕуNЕФЩЯЗНЃЌЭЌРэЧѓГіДЫЪБMNЕФзюДѓжЕЃЌШЁЖўепНЯДѓжЕЃЌМДПЩЕУГіMNЕФзюДѓжЕ.
ЃЈ1ЃЉЁпХзЮяЯпl1ЃКy=Љx2+bx+3ЖдГЦжсЮЊx=1ЃЌ
Ёрx=Љ![]() =1ЃЌb=2ЃЌ
=1ЃЌb=2ЃЌ
ЁрХзЮяЯпl1ЕФКЏЪ§БэДяЪНЮЊЃКy=Љx2+2x+3ЃЌ
ЕБy=0ЪБЃЌЉx2+2x+3=0ЃЌ
НтЕУЃКx1=3ЃЌx2=Љ1ЃЌ
ЁрAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌ
ЩшХзЮяЯпl2ЕФКЏЪ§БэДяЪНЃЛy=aЃЈxЉ5ЃЉЃЈx+1ЃЉЃЌ
АбDЃЈ0ЃЌЉ5ЃЉДњШыЕУЃКЉ5a=Љ5ЃЌa=1ЃЌ
ЁрХзЮяЯпl2ЕФКЏЪ§БэДяЪНЃЛy=x2Љ4xЉ5ЃЛ
ЃЈ2ЃЉзїCHЁЭPGНЛжБЯпPGгкЕуHЃЌ
ЩшPЕузјБъЮЊЃЈ1ЃЌyЃЉЃЌгЩЃЈ1ЃЉПЩЕУCЕузјБъЮЊЃЈ0ЃЌ3ЃЉЃЌ
ЁрCH=1ЃЌPH=|3Љy |ЃЌPG=|y |ЃЌAG=2ЃЌ
ЁрPC2=12+ЃЈ3ЉyЃЉ2=y2Љ6y+10ЃЌPA2= =y2+4ЃЌ
ЁпPC=PAЃЌ
ЁрPA2=PC2ЃЌ
Ёрy2Љ6y+10=y2+4ЃЌНтЕУy=1ЃЌ
ЁрPЕузјБъЮЊЃЈ1ЃЌ1ЃЉЃЛ
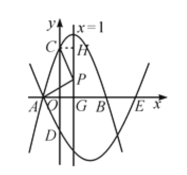
ЃЈ3ЃЉгЩЬтвтПЩЩшMЃЈxЃЌx2Љ4xЉ5ЃЉЃЌ
ЁпMNЁЮyжсЃЌ
ЁрNЃЈxЃЌЉx2+2x+3ЃЉЃЌ
СюЉx2+2x+3=x2Љ4xЉ5ЃЌПЩНтЕУx=Љ1Лђx=4ЃЌ
ЂйЕБЉ1ЃМxЁм4ЪБЃЌMN=ЃЈЉx2+2x+3ЃЉЉЃЈx2Љ4xЉ5ЃЉ=Љ2x2+6x+8=Љ2ЃЈxЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЌ
ЃЌ
ЯдШЛЉ1ЃМ![]() Ём4ЃЌ
Ём4ЃЌ
ЁрЕБx=![]() ЪБЃЌMNгазюДѓжЕ12.5ЃЛ
ЪБЃЌMNгазюДѓжЕ12.5ЃЛ
ЂкЕБ4ЃМxЁм5ЪБЃЌMN=ЃЈx2Љ4xЉ5ЃЉЉЃЈЉx2+2x+3ЃЉ=2x2Љ6xЉ8=2ЃЈxЉ![]() ЃЉ2Љ
ЃЉ2Љ![]() ЃЌ
ЃЌ
ЯдШЛЕБxЃО![]() ЪБЃЌMNЫцxЕФдіДѓЖјдіДѓЃЌ
ЪБЃЌMNЫцxЕФдіДѓЖјдіДѓЃЌ
ЁрЕБx=5ЪБЃЌMNгазюДѓжЕЃЌMN=2ЃЈ5Љ![]() ЃЉ2Љ
ЃЉ2Љ![]() =12.
=12.
злЩЯПЩжЊЃКдкЕуMздЕуAдЫЖЏжСЕуEЕФЙ§ГЬжаЃЌЯпЖЮMNГЄЖШЕФзюДѓжЕЮЊ12.5ЃЎ


 ПьРжЪюМйЪюМйФмСІздВтжаЮїЪщОжЯЕСаД№АИ
ПьРжЪюМйЪюМйФмСІздВтжаЮїЪщОжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬЃЈkЉ1ЃЉx2Љ2kx+k+2=0гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЎ
ЃЈ1ЃЉЧѓkЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєx1ЃЌx2ЪЧвЛдЊЖўДЮЗНГЬЕФСНИіЪЕЪ§ИљЃЌЧвТњзу![]() =Љ2ЃЌЧѓkЕФжЕЃЌВЂЧѓДЫЪБЗНГЬЕФНтЃЎ
=Љ2ЃЌЧѓkЕФжЕЃЌВЂЧѓДЫЪБЗНГЬЕФНтЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТСаВФСЯЃК
![]() ФъЩЯАыФъГіЬЈЙцЖЈЃЌНЋгУПеЦјжЪСПжИЪ§ЬцДњдгаЕФПеЦјЮлШОжИЪ§ЃЎПеЦјжЪСПАДееПеЦјжЪСПжИЪ§ДѓаЁЗжЮЊСљМЖЃЌЯрЖдгІПеЦјжЪСПЕФСљИіРрБ№ЃЌжИЪ§дНДѓЁЂМЖБ№дНИпЃЌЫЕУїЮлШОЕФЧщПідНбЯжиЃЌЖдШЫЬхЕФНЁПЕЮЃКІвВОЭдНДѓЃЌДгвЛМЖгХЃЌЖўМЖСМЃЌШ§МЖЧсЖШЮлШОЃЌЫФМЖжаЖШЮлШОЃЌжБжСЮхМЖжиЖШЮлШОЃЌСљМЖбЯжиЮлШОЃЎНЋПеЦјжЪСПДяЕНвЛМЖгХЃЌЖўМЖСМЕФЬьЦјЖЈвхЮЊДяБъЬьЦјЃЎ
ФъЩЯАыФъГіЬЈЙцЖЈЃЌНЋгУПеЦјжЪСПжИЪ§ЬцДњдгаЕФПеЦјЮлШОжИЪ§ЃЎПеЦјжЪСПАДееПеЦјжЪСПжИЪ§ДѓаЁЗжЮЊСљМЖЃЌЯрЖдгІПеЦјжЪСПЕФСљИіРрБ№ЃЌжИЪ§дНДѓЁЂМЖБ№дНИпЃЌЫЕУїЮлШОЕФЧщПідНбЯжиЃЌЖдШЫЬхЕФНЁПЕЮЃКІвВОЭдНДѓЃЌДгвЛМЖгХЃЌЖўМЖСМЃЌШ§МЖЧсЖШЮлШОЃЌЫФМЖжаЖШЮлШОЃЌжБжСЮхМЖжиЖШЮлШОЃЌСљМЖбЯжиЮлШОЃЎНЋПеЦјжЪСПДяЕНвЛМЖгХЃЌЖўМЖСМЕФЬьЦјЖЈвхЮЊДяБъЬьЦјЃЎ
ББОЉЪаЛЗБЃОж![]() Фъ
Фъ![]() дТ
дТ![]() ШеЩЯЮчЯђУНЬхЭЈБЈЃК
ШеЩЯЮчЯђУНЬхЭЈБЈЃК
![]() ФъББОЉПеЦјжЪСПзДПіЃЌгы
ФъББОЉПеЦјжЪСПзДПіЃЌгы![]() ФъЯрБШЃЌ
ФъЯрБШЃЌ![]() ФъЃЌББОЉИїЯюЮлШОЮяЭЌБШОљгаЫљИФЩЦЃЎОнБЈЕМЃЌ
ФъЃЌББОЉИїЯюЮлШОЮяЭЌБШОљгаЫљИФЩЦЃЎОнБЈЕМЃЌ![]() ФъББОЉПеЦјжЪСПГжајИФЩЦЃЌ
ФъББОЉПеЦјжЪСПГжајИФЩЦЃЌ![]() ФъОљХЈЖШ
ФъОљХЈЖШ![]() ЮЂПЫ/СЂЗНУзЃЌЭЌБШЯТНЕ
ЮЂПЫ/СЂЗНУзЃЌЭЌБШЯТНЕ![]() ЃЌЕЋЪЧетвЛЪ§жЕвРОЩГЌГіЙњМвБъзМ
ЃЌЕЋЪЧетвЛЪ§жЕвРОЩГЌГіЙњМвБъзМ![]() ЃЎ
ЃЎ![]() ФъЃЌББОЉПеЦјжЪСПДяБъЬьЪ§
ФъЃЌББОЉПеЦјжЪСПДяБъЬьЪ§![]() ЬьЃЌНЯ
ЬьЃЌНЯ![]() ФъдіМг
ФъдіМг![]() ЬьЃЌЦфжа
ЬьЃЌЦфжа![]() вЛМЖгХЕФЬьЪ§діМгСЫ
вЛМЖгХЕФЬьЪ§діМгСЫ![]() ЬьЃЌ
ЬьЃЌ![]() ФъББОЉгажиЮлШОЬьЃЈКЌбЯжиЮлШОЬьЃЉ
ФъББОЉгажиЮлШОЬьЃЈКЌбЯжиЮлШОЬьЃЉ![]() ЬьЃЎЦфжа
ЬьЃЎЦфжа![]() Фъ
Фъ![]() дТжС
дТжС![]() дТЕзЃЌББОЉШЋЪа
дТЕзЃЌББОЉШЋЪа![]() ХЈЖШЭЌБШЯТНЕ
ХЈЖШЭЌБШЯТНЕ![]() ЃЌПеЦјжЪСПДяБъЬьЪ§НЯШЅФъЭЌЦкдіМг
ЃЌПеЦјжЪСПДяБъЬьЪ§НЯШЅФъЭЌЦкдіМг![]() ЬьЃЌПеЦјжиЮлШОЬьЪ§ЭЌБШМѕЩй
ЬьЃЌПеЦјжиЮлШОЬьЪ§ЭЌБШМѕЩй![]() ФъБОЪаПеЦјжЪСПДяБъЬьЪ§НЯ
ФъБОЪаПеЦјжЪСПДяБъЬьЪ§НЯ![]() ФъдіМг
ФъдіМг![]() ЬьЃЌЦфжаPM2.5вЛМЖгХЕФЬьЪ§діМгСЫ
ЬьЃЌЦфжаPM2.5вЛМЖгХЕФЬьЪ§діМгСЫ![]() ЬьЃЎ
ЬьЃЎ![]() ФъБОЪа
ФъБОЪа![]() жиЮлШОЬьЃЈКЌбЯжиЮлШОЬьЃЉЪ§еМШЋФъзмЬьЪ§ЕФ
жиЮлШОЬьЃЈКЌбЯжиЮлШОЬьЃЉЪ§еМШЋФъзмЬьЪ§ЕФ![]() ЃЌЦфжадк
ЃЌЦфжадк![]() дТжаЗЂЩњжиЮлШО
дТжаЗЂЩњжиЮлШО![]() ЬьЃЌеМ
ЬьЃЌеМ![]() дТКЭ
дТКЭ![]() дТЬьЪ§ЕФ
дТЬьЪ§ЕФ![]() ЃЌгы
ЃЌгы![]() ФъЭЌЦкЯрБШдіМг
ФъЭЌЦкЯрБШдіМг![]() ЬьЃЎ
ЬьЃЎ![]() ФъББОЉЪа
ФъББОЉЪа![]() вЛМЖгХЕФЬьЪ§ДяЕН
вЛМЖгХЕФЬьЪ§ДяЕН![]() ЬьЃЌНЯ
ЬьЃЌНЯ![]() ФъМѕЩйСЫ
ФъМѕЩйСЫ![]() ЬьЃЌЕЋ
ЬьЃЌЕЋ![]() ЕМжТЕФжиЮлШОЬьЃЈКЌбЯжиЮлШОЬьЃЉЪ§УїЯдМѕЩйСЫ
ЕМжТЕФжиЮлШОЬьЃЈКЌбЯжиЮлШОЬьЃЉЪ§УїЯдМѕЩйСЫ![]() ЬьЃЌДг
ЬьЃЌДг![]() ФъЕФ
ФъЕФ![]() ЬьЯТНЕЮЊ
ЬьЯТНЕЮЊ![]() ЬьЃЎ
ЬьЃЎ
ИљОнвдЯТВФСЯНтД№ЯТСаЮЪЬтЃК
ЃЈ![]() ЃЉ
ЃЉ![]() ФъБОЪаПеЦјжЪСПДяБъЬьЪ§ЮЊ__________ЬьЃЛ
ФъБОЪаПеЦјжЪСПДяБъЬьЪ§ЮЊ__________ЬьЃЛ![]() ФъЦНОљХЈЖШЕФЙњМвБъзМЯожЕЪЧ__________ЮЂПЫ/СЂЗНУзЃЛЃЈНсЙћБЃСєећЪ§ЃЉЃЎ
ФъЦНОљХЈЖШЕФЙњМвБъзМЯожЕЪЧ__________ЮЂПЫ/СЂЗНУзЃЛЃЈНсЙћБЃСєећЪ§ЃЉЃЎ
ЃЈ![]() ЃЉбЁдёЭГМЦБэЛђЭГМЦЭМЃЌНЋ
ЃЉбЁдёЭГМЦБэЛђЭГМЦЭМЃЌНЋ![]() Фъ
Фъ![]() вЛМЖгХЬьЪ§ЕФЧщПіБэЪОГіРДЃЛдЄЙР
вЛМЖгХЬьЪ§ЕФЧщПіБэЪОГіРДЃЛдЄЙР![]() ФъББОЉЪа
ФъББОЉЪа![]() вЛМЖгХЬьЪ§дМ__________ЬьЃЎ
вЛМЖгХЬьЪ§дМ__________ЬьЃЎ
ЃЈ![]() ЃЉаЁУїДгБЈЕРжаЗЂЯжЁА
ЃЉаЁУїДгБЈЕРжаЗЂЯжЁА![]() Фъ
Фъ![]() дТжС
дТжС![]() дТЕзЃЌББОЉШЋЪа
дТЕзЃЌББОЉШЋЪа![]() ХЈЖШЭЌБШЯТНЕ
ХЈЖШЭЌБШЯТНЕ![]() ЃЌПеЦјжЪСПДяБъЬьЪ§НЯШЅФъЭЌЦкдіМг
ЃЌПеЦјжЪСПДяБъЬьЪ§НЯШЅФъЭЌЦкдіМг![]() ЬьЃЌПеЦјжиЮлШОЬьЪ§ЭЌБШМѕЩй
ЬьЃЌПеЦјжиЮлШОЬьЪ§ЭЌБШМѕЩй![]() ЬьЃЌЁБЫћгЩДЫЭЦЖЯЁА
ЬьЃЌЁБЫћгЩДЫЭЦЖЯЁА![]() ФъШЋФъЕФ
ФъШЋФъЕФ![]() ДяБъЬьЪ§ЕФФъдіГЄТЪНЋБШ
ДяБъЬьЪ§ЕФФъдіГЄТЪНЋБШ![]() ФъШЋФъЕФ
ФъШЋФъЕФ![]() ДяБъЬьЪ§ЕФФъдіГЄТЪГіЯжДѓЗљдіГЄЃЌЁБФуЭЌвтЫћЕФНсТлТ№ЃПВЂЫЕУїФуЕФРэгЩЃЎ
ДяБъЬьЪ§ЕФФъдіГЄТЪГіЯжДѓЗљдіГЄЃЌЁБФуЭЌвтЫћЕФНсТлТ№ЃПВЂЫЕУїФуЕФРэгЩЃЎ
ЃЈ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвЛдЊЖўДЮЗНГЬЃЈa+1ЃЉx2Љax+a2ЉaЉ2=0ЕФвЛИіИљгыЗНГЬЃЈa+1ЃЉx2+axЉa2+a+2=0ЕФвЛИіИљЛЅЮЊЯрЗДЪ§ЃЌФЧУДЃЈa+1ЃЉx2+axЉa2+a+2=0ЕФИљЪЧЃЈЁЁЁЁЃЉ
A. 0ЃЌЉ![]() B. 0ЃЌ
B. 0ЃЌ![]() C. Љ1ЃЌ2 D. 1ЃЌЉ2
C. Љ1ЃЌ2 D. 1ЃЌЉ2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіПкДќжага3ИіДѓаЁЯрЭЌЕФаЁЧђЃЌЧђУцЩЯЗжБ№аДгаЪ§зж1ЁЂ2ЁЂ3ЃЎДгДќжаЫцЛњЕиУўГівЛИіаЁЧђЃЌМЧТМЯТЪ§зжКѓЗХЛиЃЌдйЫцЛњЕиУўГівЛИіаЁЧђЃЎ
ЃЈ1ЃЉЧыгУЪїаЮЭМЛђСаБэЗЈжаЕФвЛжжЃЌСаОйГіСНДЮУўГіЕФЧђЩЯЪ§зжЕФЫљгаПЩФмНсЙћЃЛ
ЃЈ2ЃЉЧѓСНДЮУўГіЕФЧђЩЯЕФЪ§зжКЭЮЊХМЪ§ЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввЁЂБћШ§ЮЛдЫЖЏдБдкЯрЭЌЬѕМўЯТИїЩфАа![]() ДЮЃЌУПДЮЩфАаЕФГЩМЈШчЯТЃК
ДЮЃЌУПДЮЩфАаЕФГЩМЈШчЯТЃК
МзЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
ввЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
БћЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
ЃЈ1ЃЉИљОнвдЩЯЪ§ОнЭъГЩЯТБэЃК
ЦНОљЪ§ | жаЮЛЪ§ | ЗНВю | |
Мз |
|
| __________ |
вв | __________ |
|
|
Бћ |
| __________ |
|
ЃЈ2ЃЉИљОнБэжаЪ§ОнЗжЮіЃЌФФЮЛдЫЖЏдБЕФГЩМЈзюЮШЖЈ.ВЂМђвЊЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌГЄЗНаЮ![]() ЕФЯюЕу
ЕФЯюЕу![]() ЕФзјБъЪЧ
ЕФзјБъЪЧ![]() .
.

ЃЈ1ЃЉжБНгаДГі![]() ЕузјБъЃЈ______ЃЌ______ЃЉЃЌ
ЕузјБъЃЈ______ЃЌ______ЃЉЃЌ![]() ЕузјБъЃЈ______ЃЌ______ЃЉЃЛ
ЕузјБъЃЈ______ЃЌ______ЃЉЃЛ
ЃЈ2ЃЉШчЭМЃЌDЮЊ![]() жаЕу.СЌНг
жаЕу.СЌНг![]() ЃЌ
ЃЌ![]() ЃЌШчЙћдкЕкЖўЯѓЯоФкгавЛЕу
ЃЌШчЙћдкЕкЖўЯѓЯоФкгавЛЕу![]() ЃЌЧвЫФБпаЮ
ЃЌЧвЫФБпаЮ![]() ЕФУцЛ§ЪЧ
ЕФУцЛ§ЪЧ![]() УцЛ§ЕФ
УцЛ§ЕФ![]() БЖЃЌЧѓТњзуЬѕМўЕФЕу
БЖЃЌЧѓТњзуЬѕМўЕФЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ

ЃЈ3ЃЉШчЭМЃЌЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌвдУПГЎ
ГіЗЂЃЌвдУПГЎ![]() ИіЕЅЮЛЕФЫйЖШбиЯпЖЮ
ИіЕЅЮЛЕФЫйЖШбиЯпЖЮ![]() дЫЖЏЃЌЭЌЪБЖЏЕу
дЫЖЏЃЌЭЌЪБЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂ.вдУПУы
ГіЗЂ.вдУПУы![]() ИіЕЅЮЛЕФпBЖШбиЯпЖЮ
ИіЕЅЮЛЕФпBЖШбиЯпЖЮ![]() дЫЖЏЃЌЕБ
дЫЖЏЃЌЕБ![]() ЕНДя
ЕНДя![]() ЕуЪБЃЌ
ЕуЪБЃЌ![]() ЃЌ
ЃЌ![]() ЭЌЪБЭЃжЙдЫЖЏЃЌдЫЖЏЪБМфЪЧ
ЭЌЪБЭЃжЙдЫЖЏЃЌдЫЖЏЪБМфЪЧ![]() Уы
Уы![]() ЃЌдк
ЃЌдк![]() ЃЌ
ЃЌ![]() дЫЖЏЙ§ГЬжа.ЕБ
дЫЖЏЙ§ГЬжа.ЕБ![]() ЪБЃЌжБНгаДГіЪБМф
ЪБЃЌжБНгаДГіЪБМф![]() ЕФжЕ.
ЕФжЕ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ1ЪЧвЛИіживЊЙЋЪНЕФМИКЮНтЪЭЃЎЧыФуаДГіетИіЙЋЪНЃК ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() Ш§ЕуЙВЯп.
Ш§ЕуЙВЯп.
ЪджЄУї![]() ЃЛ
ЃЛ

ЃЈ3ЃЉЙДЙЩЖЈРэЪЧМИКЮбЇжаЕФУїжщЃЌЧЇАйФъРДЃЌШЫУЧЖдЫќЕФжЄУїЧїжЎШєц№ЃЌгазЪСЯБэУїЃЌЙигкЙДЙЩЖЈРэЕФжЄУїЗНЗЈвбга500гржж.ПЮБОжаНщЩмСЫБШНЯгаДњБэадЕФедЫЌЯвЭМ.
йЄЗЦЖћЕТЃЈGarfieldЃЌ1881ФъШЮУРЙњЕк20НьзмЭГЃЉРћгУЭМ2жЄУїСЫЙДЙЩЖЈРэЃЈ1876Фъ4дТ1ШеЃЌЗЂБэдкЁЖаТгЂИёРМНЬг§ШежОЁЗЩЯЃЉЃЌЧыФуаДГіИУжЄУїЙ§ГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃАЫФъМЖЙВгаШ§ИіАрЃЌЖМВЮМгСЫбЇаЃОйааЕФЪщЗЈЛцЛДѓШќЃЌШ§ИіАрИљОнГѕШќГЩМЈЗжБ№бЁГіСЫ10УћЭЌбЇВЮМгОіШќЃЌетаЉбЁЪжЕФОіШќГЩМЈ(ТњЗж100Зж)ШчЯТБэЫљЪОЃК
ОіШќГЩМЈ(ЕЅЮЛЃКЗж) | |
АЫФъ1Ар | 80ЁЁЁЁ86ЁЁЁЁ88ЁЁЁЁ80ЁЁЁЁ88ЁЁЁЁ99ЁЁЁЁ80ЁЁЁЁ74ЁЁЁЁ91ЁЁЁЁ89 |
АЫФъ2Ар | 85ЁЁЁЁ85ЁЁЁЁ87ЁЁЁЁ97ЁЁЁЁ85ЁЁЁЁ76ЁЁЁЁ88ЁЁЁЁ77ЁЁЁЁ87ЁЁЁЁ88 |
АЫФъ3Ар | 82ЁЁЁЁ80ЁЁЁЁ78ЁЁЁЁ78ЁЁЁЁ81ЁЁЁЁ96ЁЁЁЁ97ЁЁЁЁ87ЁЁЁЁ92ЁЁЁЁ84 |
НтД№ЯТСаЮЪЬтЃК
(1)ЧыЬюаДЯТБэЃК
ЦНОљЪ§(Зж) | жкЪ§(Зж) | жаЮЛЪ§(Зж) | |
ЁЁАЫФъ1Ар | 85.5 | ЁЁ ЁЁ | 87 |
ЁЁАЫФъ2Ар | 85.5 | 85 | ЁЁ ЁЁ |
ЁЁАЫФъ3Ар | ЁЁ ЁЁ | 78 | 83 |
(2)ЧыДгвдЯТСНИіВЛЭЌЕФНЧЖШЖдШ§ИіАрМЖЕФОіШќГЩМЈНјаа
ЂйДгЦНОљЪ§КЭжкЪ§ЯрНсКЯПД(ЗжЮіФФИіАрМЖГЩМЈКУаЉ)ЃЎ
ЂкДгЦНОљЪ§КЭжаЮЛЪ§ЯрНсКЯПД(ЗжЮіФФИіАрМЖГЩМЈКУаЉ)ЃЎ
(3)ШчЙћдкУПИіАрМЖВЮМгОіШќЕФбЁЪжжаЗжБ№бЁГі3ШЫВЮМгзмОіШќЃЌФуШЯЮЊФФИіАрМЖЕФЪЕСІИќЧПвЛаЉЃПЧыМђвЊЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com