
【题目】已知一元二次方程(a+1)x2﹣ax+a2﹣a﹣2=0的一个根与方程(a+1)x2+ax﹣a2+a+2=0的一个根互为相反数,那么(a+1)x2+ax﹣a2+a+2=0的根是( )
A. 0,﹣![]() B. 0,
B. 0,![]() C. ﹣1,2 D. 1,﹣2
C. ﹣1,2 D. 1,﹣2
 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
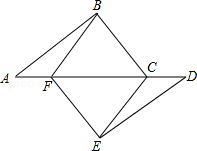
【题目】如图,点A.F、C.D在同一直线上,点B和点E分别在直线AD的两侧,且
AB=DE,∠A=∠D,AF=DC.
(1)求证:四边形BCEF是平行四边形,
(2)若∠ABC=90°,AB=4,BC=3,当AF为何值时,四边形BCEF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,三阶幻方是由1,2,3,4,5,6,7,8,9九个数字组成的一个三行三列的数表,要求其对角线、横行、纵向的和都相等。即为15,称这个幻方的幻和为15。四阶幻方是由1,2,3,……,15,16十六个数组成一个四行四列的数表,其对角线、横向、纵向的和都为同一个数,此数称为四阶幻方的幻和,那么此四阶幻方的幻和等于_________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地间的直线公路长为![]() 千米.一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行,货车比轿车早出发
千米.一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行,货车比轿车早出发![]() 小时,途中轿车出现了故障,停下维修,货车仍继续行驶.
小时,途中轿车出现了故障,停下维修,货车仍继续行驶.![]() 小时后轿车故障被排除,此时接到通知,轿车立刻掉头按原路原速返回甲地(接到通知及掉头时间不计).最后两车同时到达甲地,已知两车距各自出发地的距离
小时后轿车故障被排除,此时接到通知,轿车立刻掉头按原路原速返回甲地(接到通知及掉头时间不计).最后两车同时到达甲地,已知两车距各自出发地的距离![]() (千米)与轿车所用的时间
(千米)与轿车所用的时间![]() (小时)的关系如图所示,请结合图象解答下列问题:
(小时)的关系如图所示,请结合图象解答下列问题:
(1)货车的速度是_______千米/小时;轿车的速度是_______千米/小时;![]() 值为_______.
值为_______.
(2)求轿车距其出发地的距离![]() (千米)与所用时间
(千米)与所用时间![]() (小时)之间的函数关系式并写出自变量
(小时)之间的函数关系式并写出自变量![]() 的取值范围;
的取值范围;
(3)请直接写出货车出发多长时间两车相距![]() 千米.
千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某小区小孩暑期的学习情况,王老师随机调查了该小区8个小孩某天的学习时间,结果如下(单位:小时):1.5,1.5,3,4,2,5,2.5,4.5,关于这组数据,下列结论错误的是( )
A. 极差是3.5 B. 众数是1.5 C. 中位数是3 D. 平均数是3
查看答案和解析>>
科目:初中数学 来源: 题型:
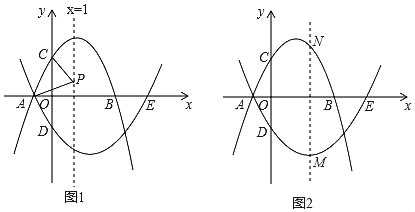
【题目】如图1,抛物线l1:y=﹣x2+bx+3交x轴于点A、B,(点A在点B的左侧),交y轴于点C,其对称轴为x=1,抛物线l2经过点A,与x轴的另一个交点为E(5,0),交y轴于点D(0,﹣5).
(1)求抛物线l2的函数表达式;
(2)P为直线x=1上一动点,连接PA、PC,当PA=PC时,求点P的坐标;
(3)M为抛物线l2上一动点,过点M作直线MN∥y轴(如图2所示),交抛物线l1于点N,求点M自点A运动至点E的过程中,线段MN长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,正方形ABCD的边AB在x轴上,A(﹣4,0),B(﹣2,0),定义:若某个抛物线上存在一点P,使得点P到正方形ABCD四个顶点的距离相等,则称这个抛物线为正方形ABCD的“友好抛物线”.若抛物线y=2x2﹣nx﹣n2﹣1是正方形ABCD的“友好抛物线”,则n的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A﹙-2,-5﹚、C﹙5,n﹚,交y轴于点B,交x轴于点D.
的图象交于点A﹙-2,-5﹚、C﹙5,n﹚,交y轴于点B,交x轴于点D.
(1)求反比例函数y=![]() 和一次函数y=kx+b的表达式;
和一次函数y=kx+b的表达式;
(2)连接OA、OC,求△AOC的面积;
(3)写出使一次函数的值大于反比例函数的x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com