
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A﹙-2,-5﹚、C﹙5,n﹚,交y轴于点B,交x轴于点D.
的图象交于点A﹙-2,-5﹚、C﹙5,n﹚,交y轴于点B,交x轴于点D.
(1)求反比例函数y=![]() 和一次函数y=kx+b的表达式;
和一次函数y=kx+b的表达式;
(2)连接OA、OC,求△AOC的面积;
(3)写出使一次函数的值大于反比例函数的x的取值范围.

【答案】(1)y=![]() ;y=x﹣3;(2)10.5;(3)﹣2<x<0或x>5;
;y=x﹣3;(2)10.5;(3)﹣2<x<0或x>5;
【解析】
(1)把A(﹣2,﹣5)代入y=![]() 求得m的值,然后求得C的坐标,利用待定系数法求得直线的解析式即可;(2)先求得OB的长,再根据S△AOC=S△AOB+S△BOC即可求得△AOC的面积;(3)根据图象和交点坐标即可求得.
求得m的值,然后求得C的坐标,利用待定系数法求得直线的解析式即可;(2)先求得OB的长,再根据S△AOC=S△AOB+S△BOC即可求得△AOC的面积;(3)根据图象和交点坐标即可求得.
(1)把点A(﹣2,﹣5)代入反比例函数的解析式y=![]() 得:﹣5=
得:﹣5=![]() ,
,
解得:m=10,
即反比例函数的解析式为:y=![]() ,
,
把点C(5,n)代入解析式y=![]() 得:n=2,
得:n=2,
即点C的坐标为(5,2),
把点A(﹣2,﹣5)和点C(5,2)代入y=kx+b得:
![]() ,
,
解得:![]() ,
,
即一次函数的表达式为y=x﹣3,
(2)把x=0代入y=x﹣3得:y=﹣3,
即OB=3,
∵C(5,2),A﹙-2,-5﹚,
∴S△AOC=S△AOB+S△BOC=![]() OB|2|+
OB|2|+![]() OB5=
OB5=![]() OB(2+5)=10.5.
OB(2+5)=10.5.
(3)通过观察图象可知:
使一次函数的值大于反比例函数的x的取值范围为:﹣2<x<0或x>5.


科目:初中数学 来源: 题型:
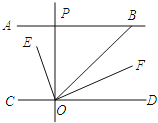
【题目】如图,![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,![]() ,有下列结论:
,有下列结论:
①![]() ;②
;②![]() 平分
平分![]() ;③
;③![]() ;④
;④![]() .
.
请将正确结论的序号填写在空中,并选择其一证明.
正确结论的序号是______,我选择证明的结论序号是______,证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.
根据以上信息回答下列问题:
最喜爱的趣味运动项目类型频数分布表:
项目类型 | 频数 | 频率 |
跳长绳 | 25 | a |
踢毽子 | 20 | 0.2 |
背夹球 | b | 0.4 |
拔河 | 15 | 0.15 |
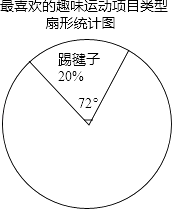
(1)直接写出a= , b=;
(2)利用频数分布表中的数据,在图中绘制扇形统计图(注明项目、百分比、圆心角);
(3)若全校共有学生1200名,估计该校最喜爱背夹球和拔河的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的三个顶点的坐标分别是
的三个顶点的坐标分别是![]() ,将
,将![]() 先向右平移
先向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位长度得到
个单位长度得到![]() .
.

(1)在平面直角坐标系中,画出平移后的![]() ;
;
(2)求出![]() 的面积;
的面积;
(3)点![]() 是
是![]() 轴上的一点,若
轴上的一点,若![]() 的面积等于
的面积等于![]() 的面积,求点
的面积,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了适应广大市民锻炼,休闲的需要,某市新修建了一条绿道![]() (如图),父子两人同时从起点
(如图),父子两人同时从起点![]() 出发,沿绿道进行跑步锻炼,到达
出发,沿绿道进行跑步锻炼,到达![]() 点后立即返回向起点
点后立即返回向起点![]() 跑去,他们不断往返于
跑去,他们不断往返于![]() 之间,已知父子两人的速度分别为2米/秒和3米/秒,儿子第一次到达
之间,已知父子两人的速度分别为2米/秒和3米/秒,儿子第一次到达![]() 点时,父亲离
点时,父亲离![]() 点还有1200米,则(1)父亲第一次到达
点还有1200米,则(1)父亲第一次到达![]() 点时,儿子离
点时,儿子离![]() 点的距离是_________米;(2)从起点
点的距离是_________米;(2)从起点![]() 出发后________小时父子两人恰好第一次同时回到起点
出发后________小时父子两人恰好第一次同时回到起点![]() .
.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,第n次操作后,得到△AnBnCn,要使△AnBnCn的面积超过2020,则至少需要操作__________次.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成证明并写出推理根据:如图,直线![]() 分别与直线
分别与直线![]() 、
、![]() 交于点
交于点![]() 和点
和点![]() ,
,![]() ,射线
,射线![]() 、
、![]() 分别与直线
分别与直线![]() 交于点
交于点![]() 、
、![]() ,且
,且![]() ,则
,则![]() 与
与![]() 有何数量关系?并说明理由.
有何数量关系?并说明理由.

解:![]() 与
与![]() 的数量关系为 ① ,理由如下:
的数量关系为 ① ,理由如下:
∵![]() (已知)
(已知)
∴ ② // ② ( ② )
∴![]() ③ ( ③ )
③ ( ③ )
∵![]() (已知)
(已知)
∴ ④ ( ④ )
∵![]() ⑤
⑤
∴![]() ⑥ -
⑥ -![]() ⑥
⑥
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com