练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，点D、E分别为BC、AD的中点，EF=2FC，若△ABC的面积为12 cm2，则△BEF的面积为（ ）

    A.B.C.D.

    【答案】C

    【解析】

    由点D是BC的中点，可得△ABD的面积=△ACD的面积=△ABC，由E是AD的中点，得出△ABE的面积=△D BE的面积=△ABC的面积，进而得出△BCE的面积=△ABC的面积，再利用EF=2FC，求出△BEF的面积.

    点D是BC的中点，△ABD的面积=△ACD的面积=△ABC的面积= 6，

    E是AD的中点，△ABE的面积=△DBE的面积=△ABC的面积= 3，

    △ACE的面积=△DCE的面积=△ABC的面积= 3，

    △BCE的面积=△ABC的面积= 6,

    EF= 2FC，△BEF的面积=6=4.

    故选C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，在正方形ABCD中，E，F分别是AD，CD上两点，BE交AF于点G，且DE＝CF．

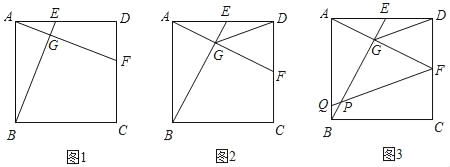
    （1）写出BE与AF之间的关系，并证明你的结论；

    （2）如图2，若AB＝2，点E为AD的中点，连接GD，试证明GD是∠EGF的角平分线，并求出GD的长；

    （3）如图3，在（2）的条件下，作FQ∥DG交AB于点Q，请直接写出FQ的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数y=kx+b的图象与反比例函数y=的图象交于点A﹙－2，－5﹚、C﹙5，n﹚，交y轴于点B，交x轴于点D．

    (1)求反比例函数y=和一次函数y=kx+b的表达式；

    (2)连接OA、OC，求△AOC的面积；

    (3)写出使一次函数的值大于反比例函数的x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，BC＝10，BC边上的高为3．将点A绕点B逆时针旋转90°得到点E，绕点C顺时针旋转90°得到点D．沿BC翻折得到点F，从而得到一个凸五边形BFCDE，则五边形BFCDE的面积为_____．

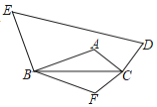
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】装饰公司为小明家设计电视背景墙时需要A、B型板材若干块，A型板材规格是ab，B型板材规格是bb．现只能购得规格是150b的标准板材．（单位：cm）

    （1）若设a60cm，b30cm．一张标准板材尽可能多的裁出A型、B型板材，共有下表三种裁法，下图是裁法一的裁剪示意图．

    裁法一

    裁法二

    裁法三

    A型板材块数

    1

    2

    0

    B型板材块数

    3

    m

    n

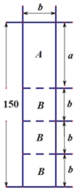
    则上表中， m=___________， n=__________；

    （2）为了装修的需要，小明家又购买了若干C型板材，其规格是aa，并做成如下图的背景墙．请写出下图中所表示的等式：__________；

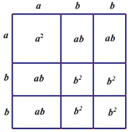
    (3)若给定一个二次三项式2a25ab3b2，试用拼图的方式将其因式分解．（请仿照（2）在几何图形中标上有关数量）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，P是正三角形ABC内的一点，且PA＝6，PB＝8，PC＝10．若将△PAC绕点A逆时针旋转后，得到△P′AB．

    （1）求点P与点P′之间的距离；

    （2）求∠APB的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】完成下列证明

    如图，点D，E，F分别在AB，BC，AC上，且DE//AC，EF//AB

    求证：∠A+∠B+∠C=180°

    证明：∵DE//AC，

    ∴∠1=________，∠4=________（ ）

    又∵EF//AB，

    ∴∠3=________（ ）

    ∠2=________（ ）

    ∴∠2=∠A（ ）

    又∵∠1+∠2+∠3=180°（平角定义）

    ∴∠A+∠B+∠C=180°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】疫情期间，学校为了学生在班级将生活垃圾和废弃口罩分类丢弃，准备购买A,B两种型号的垃圾箱，通过市场调研得知：购买3个A型垃圾箱和2个B型垃圾箱共需270元，购买2个A型垃圾箱比购买3个B型垃圾箱少用80元．求每个A型垃圾箱和B型垃圾箱各多少元？学校购买A型垃圾桶8个，B型垃圾桶16个，共花费多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，正方形A1B1C1O、A2B2C2B1、A3B3C3B2 ， …，按图所示的方式放置．点A1、A2、A3 ， …和点B1、B2、B3 ， …分别在直线y=kx+b和x轴上．已知C1（1，﹣1），C2（ ， ），则点A3的坐标是 ．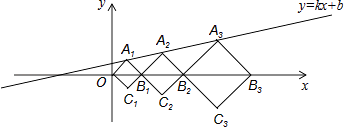

    查看答案和解析>>

    同步练习册答案