
【题目】完成下列证明
如图,点D,E,F分别在AB,BC,AC上,且DE//AC,EF//AB

求证:∠A+∠B+∠C=180°
证明:∵DE//AC,
∴∠1=________,∠4=________( )
又∵EF//AB,
∴∠3=________( )
∠2=________( )
∴∠2=∠A( )
又∵∠1+∠2+∠3=180°(平角定义)
∴∠A+∠B+∠C=180°
科目:初中数学 来源: 题型:
【题目】某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.
根据以上信息回答下列问题:
最喜爱的趣味运动项目类型频数分布表:
项目类型 | 频数 | 频率 |
跳长绳 | 25 | a |
踢毽子 | 20 | 0.2 |
背夹球 | b | 0.4 |
拔河 | 15 | 0.15 |
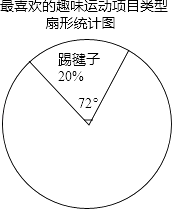
(1)直接写出a= , b=;
(2)利用频数分布表中的数据,在图中绘制扇形统计图(注明项目、百分比、圆心角);
(3)若全校共有学生1200名,估计该校最喜爱背夹球和拔河的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+4经过A(﹣3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC,有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时另一个动点Q从点C出发,沿线段CA以某一速度向点A移动.
(1)求该抛物线的解析式;
(2)若经过t秒的移动,线段PQ被CD垂直平分,求此时t的值;
(3)该抛物线的对称轴上是否存在一点M,使MQ+MA的值最小?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③2S四边形AEPF=S△ABC;④BE+CF=EF.上述结论中始终正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名学生练习计算机打字,甲打一篇1000字的文章与乙打一篇800字的文章所用的时间相同.已知甲每分钟比乙每分钟多打10个字.求甲、乙两人每分钟各打多少字?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成证明并写出推理根据:如图,直线![]() 分别与直线
分别与直线![]() 、
、![]() 交于点
交于点![]() 和点
和点![]() ,
,![]() ,射线
,射线![]() 、
、![]() 分别与直线
分别与直线![]() 交于点
交于点![]() 、
、![]() ,且
,且![]() ,则
,则![]() 与
与![]() 有何数量关系?并说明理由.
有何数量关系?并说明理由.

解:![]() 与
与![]() 的数量关系为 ① ,理由如下:
的数量关系为 ① ,理由如下:
∵![]() (已知)
(已知)
∴ ② // ② ( ② )
∴![]() ③ ( ③ )
③ ( ③ )
∵![]() (已知)
(已知)
∴ ④ ( ④ )
∵![]() ⑤
⑤
∴![]() ⑥ -
⑥ -![]() ⑥
⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是边长为4的正方形,点E在边AD所在直线上,连接CE,以CE为边,作正方形CEFG(C、E、F、G按顺时针排列),连接BF.
(1)如图1,当点E与点A重合时,请直接写出BF的长;
(2)如图2,当点E在线段AD上时,AE=1,求BF的长;
(3)若BG3![]() ,请求出此时AE的长.
,请求出此时AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com