练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】为了解某小区小孩暑期的学习情况，王老师随机调查了该小区8个小孩某天的学习时间，结果如下（单位：小时）：1.5，1.5，3，4，2，5，2.5，4.5，关于这组数据，下列结论错误的是（　　）

    A. 极差是3.5 B. 众数是1.5 C. 中位数是3 D. 平均数是3

    【答案】C

    【解析】

    由极差、众数、中位数、平均数的定义对四个选项一一判断即可.

    A.极差为5﹣1.5=3.5，此选项正确；

    B.1.5个数最多，为2个，众数是1.5，此选项正确；

    C.将式子由小到大排列为：1.5，1.5，2，2.5，3，4，4.5，5，中位数为×（2.5+3）=2.75，此选项错误；

    D.平均数为：×（1.5+1.5+2+2.5+3+4+4.5+5）=3，此选项正确.

    故选C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（问题背景）

    如图，在平面直角坐标系中，点的坐标是，点是轴上的一个动点.当点在轴上移动时，始终保持是等腰直角三角形，且(点、、按逆时针方向排列)；当点移动到点时，得到等腰直角三角形(此时点与点重合).

    （初步探究）

    (1)写出点的坐标______.

    (2)点在轴上移动过程中，当等腰直角三角形的顶点在第四象限时，连接.

    求证：；

    （深入探究）

    (3)当点在轴上移动时，点也随之运动.经过探究发现，点的横坐标总保持不变，请直接写出点的横坐标：______.

    （拓展延伸）

    (4)点在轴上移动过程中，当为等腰三角形时，直接写出此时点的坐标.

    备用图

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于平面直角坐标系中的任意两点，，我们把叫，两点间的“平面距离”，记作．

    （）已知为坐标原点，动点是坐标轴上的点，满足，请写出点的坐标．答：__________．

    （）设是平面上一点，是直线上的动点，我们定义的最小值叫做到直线的“平面距离”．试求点到直线的“平面距离”．

    （）在上面的定义基础上，我们可以定义平面上一条直线与⊙的“直角距离”：在直线与⊙上各自任取一点，此两点之间的“平面距离”的最小值称为直线与⊙的“平面距离”，记作．

    试求直线与圆心在直线坐标系原点、半径是的⊙的直角距离__________．（直接写出答案）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】请阅读下列材料：

    问题：如图，在正方形和平行四边形中，点，，在同一条直线上，是线段的中点，连接，．

    探究：当与的夹角为多少度时，平行四边形是正方形？

    小聪同学的思路是：首先可以说明四边形是矩形；然后延长交于点，构造全等三角形，经过推理可以探索出问题的答案．

    请你参考小聪同学的思路，探究并解决这个问题．

    （1）求证：四边形是矩形；

    （2）与的夹角为________度时，四边形是正方形．

    理由：

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一元二次方程（a+1）x2﹣ax+a2﹣a﹣2=0的一个根与方程（a+1）x2+ax﹣a2+a+2=0的一个根互为相反数，那么（a+1）x2+ax﹣a2+a+2=0的根是（　　）

    A. 0，﹣ B. 0， C. ﹣1，2 D. 1，﹣2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为美化校园，计划对面积为1800m2的区域进行绿化，安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍，并且在独立完成面积为400 m2区域的绿化时，甲队比乙队少用4天.

    （1）求甲、乙两工程队每天能完成绿化的面积分别是多少m2？

    （2）若学校每天需付给甲队的绿化费用是0.4万元，乙队为0.25万元，要使这次的绿化总费用不超过8万元，至少应安排甲队工作多少天？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙、丙三位运动员在相同条件下各射靶次，每次射靶的成绩如下：

    甲：，，，，，，，，，

    乙：，，，，，，，，，

    丙：，，，，，，，，，

    （1）根据以上数据完成下表：

    平均数

    中位数

    方差

    甲

    __________

    乙

    __________

    丙

    __________

    （2）根据表中数据分析，哪位运动员的成绩最稳定.并简要说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

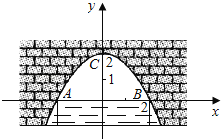
    【题目】图中是抛物线形拱桥，当拱顶离水面2m时，水面宽4m，建立如图所示的平面直角坐标系：

    （1）求拱桥所在抛物线的解析式；

    （2）当水面下降1m时，则水面的宽度为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线l1：y=﹣x与反比例函数y=的图象交于A，B两点（点A在点B左侧），已知A点的纵坐标是2：

    （1）求反比例函数的表达式；

    （2）将直线l1：y=﹣x向上平移后的直线l2与反比例函数y=在第二象限内交于点C，如果△ABC的面积为30，求平移后的直线l2的函数表达式．

    查看答案和解析>>

    同步练习册答案