
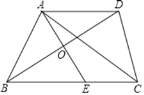
【题目】如图,在△ABC中,BD平分∠ABC,AE⊥BD于点O,交BC于点E,AD∥BC,连接CD,
(1)求证:AD=BE;
(2)当△ABC满足什么条件时四边形ABED是正方形?请说明理由.
【答案】(1)详见解析;(2)当△ABC满足∠ABC=90°时,四边形AECD是正方形.理由见解析.
【解析】
(1)判定△AOD≌△EOB,即可得到结论;
(2)先判定四边形ABED是菱形,可得当∠ABC=90°时,菱形ABED是正方形,据此可得结论.
(1)证明:∵AD∥BC,
∴∠CBD=∠ADB,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
又∵AE⊥BD,
∴BO=DO,
又∵∠AOD=∠EOB,
∴△AOD≌△EOB,
∴AD=EB;
(2)当△ABC满足∠ABC=90°时,四边形AECD是正方形.理由:
∵△AOD≌△EOB,
∴AD=BE,
又∵AD∥BE,AE⊥BD,
∴四边形ABED是菱形,
∴当∠ABC=90°时,菱形ABED是正方形,
即当△ABC满足∠ABC=90°时,四边形AECD是正方形.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
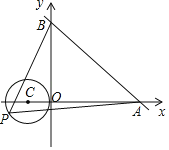
【题目】如图,直线y=﹣![]() x+6与x轴、y轴分别交于A、B两点,点P是以C(﹣1,0)为圆心,1为半径的圆上一点,连接PA,PB,则△PAB面积的最大值为_____.
x+6与x轴、y轴分别交于A、B两点,点P是以C(﹣1,0)为圆心,1为半径的圆上一点,连接PA,PB,则△PAB面积的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
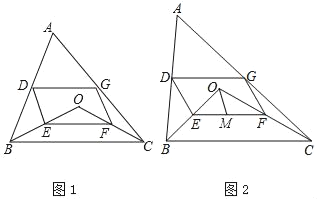
【题目】如图1,点D、E、F、G分别为线段AB、OB、OC、AC的中点.
(1)求证:四边形DEFG是平行四边形;
(2)如图2,若点M为EF的中点,BE:CF:DG=2:3:![]() ,求证:∠MOF=∠EFO.
,求证:∠MOF=∠EFO.
查看答案和解析>>
科目:初中数学 来源: 题型:
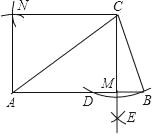
【题目】如图,已知等腰△ABC中,AB=AC.以C为圆心,CB的长为半径作弧,交AB于点D.分别以B、D为圆心,大于![]() BD的长为半径作弧,两弧交于点E.作射线CE交AB于点M.分别以A、C为圆心,CM、AM的长为半径作弧,两弧交于点N.连接AN、CN
BD的长为半径作弧,两弧交于点E.作射线CE交AB于点M.分别以A、C为圆心,CM、AM的长为半径作弧,两弧交于点N.连接AN、CN
(1)求证:AN⊥CN
(2)若AB=5,tanB=3,求四边形AMCN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
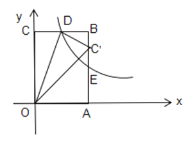
【题目】如图,平面直角坐标系中,矩形ABCD与双曲线![]() 交于D、E两点,将△OCD沿OD翻折,点C的对称C'恰好落在边AB上,已知OA=3,OC=5,则AE长为()
交于D、E两点,将△OCD沿OD翻折,点C的对称C'恰好落在边AB上,已知OA=3,OC=5,则AE长为()
A. 4B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的“相似对角线”.
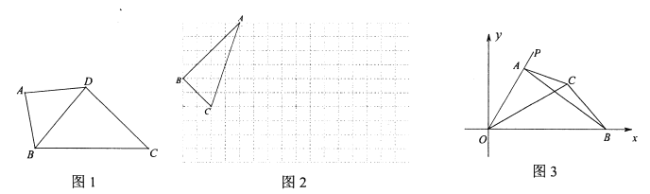
(1)如图1,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,对角线
,对角线![]() 平分
平分![]() .求证:
.求证:![]() 是四边形
是四边形![]() 的“相似对角线”;
的“相似对角线”;
(2)如图2,已知格点![]() ,请你在正方形网格中画出所有的格点四边形
,请你在正方形网格中画出所有的格点四边形![]() ,使四边形
,使四边形![]() 是以
是以![]() 为“相似对角线”的四边形;(注:顶点在小正方形顶点处的多边形称为格点多边形)
为“相似对角线”的四边形;(注:顶点在小正方形顶点处的多边形称为格点多边形)
(3)如图3,四边形![]() 中,点
中,点![]() 在射线
在射线![]() :
:![]() 上,点
上,点![]() 在
在![]() 轴正半轴上,对角线
轴正半轴上,对角线![]() 平分
平分![]() ,连接
,连接![]() .若
.若![]() 是四边形
是四边形![]() 的“相似对角线”,
的“相似对角线”,![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车和一辆快车沿相同路线从A地到B地,所行驶的路程与时间的函数图象如图所示,下列说法正确的有()个
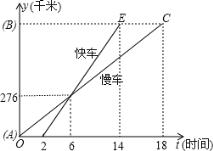
①快车追上慢车需6小时
②慢车比快车早出发2小时
③快车速度为46km/h
④慢车速度为46km/h
⑤AB两地相距828km
⑥快车14小时到达B地
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=y1+y2,其中y1与x成反比例,y2与x﹣2成正比例,函数的自变量x的取值范围是x≥![]() ,且当x=1或x=4时,y的值均为
,且当x=1或x=4时,y的值均为![]() .
.
请对该函数及其图象进行如下探究:
(1)解析式探究:根据给定的条件,可以确定出该函数的解析式为: .
(2)函数图象探究:
①根据解析式,补全下表:
x |
| 1 |
| 2 |
| 3 | 4 | 6 | 8 | … |
y |
|
|
|
|
|
|
| … |
②根据表中数据,在如图所示的平面直角坐标系中描点,并画出函数图象.

(3)结合画出的函数图象,解决问题:
①当x=![]() ,
,![]() ,8时,函数值分别为y1,y2,y3,则y1,y2,y3的大小关系为: ;(用“<”或“=”表示)
,8时,函数值分别为y1,y2,y3,则y1,y2,y3的大小关系为: ;(用“<”或“=”表示)
②若直线y=k与该函数图象有两个交点,则k的取值范围是 ,此时,x的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com