
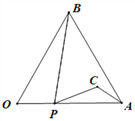
【题目】如图,等边△AOB的边长为4,点P从点O出发,沿OA以每秒1个单位的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段BP的中点绕点P按顺时针方向旋转60°得点C,点C随点P的运动而运动,连接CP、CA.在点P从O向A运动的过程中,当△PCA为直角三角形时t的值为___________.
【答案】2或![]()
【解析】如图(1)过点P作PD⊥OB于点D,过C作CE⊥OA于E,∴∠PDO=∠PEC=90°,
∵∠O=60°,∴∠OPD=30°,∴OD=![]() t,∴BD=4-
t,∴BD=4-![]() t,PD=
t,PD=![]() t,
t,
∵线段BP的中点绕点P按顺时针方向旋转60°得点C,
∴∠BPC=60°,BP=2PC,∵∠OPD=30°,
∴∠BPD+∠CPE=90°,∴∠DBP=∠CPE,
∴△PCE∽△BPD,
∴![]() ,
,
∴ ,
,
∴CE=![]() t,PE=2-
t,PE=2-![]() t,OE=2+
t,OE=2+![]() t,
t,
如图(2)当∠PCA=90度时,作CF⊥PA,∴△PCF∽△ACF,∴△PCF∽△ACF,∴![]() ,∴CF2=PFAF,
,∴CF2=PFAF,
∵PF=2-![]() t,AF=4-OF=2-
t,AF=4-OF=2-![]() t, CF=
t, CF=![]() t,
t,
∴(![]() t)2=(2-
t)2=(2-![]() t)(=2-
t)(=2-![]() t),
t),
∴t=2,这时P是OA的中点;
如图(3)当∠CAP=90°时,此时OA=OE,
∴2+![]() t=4,∴t=
t=4,∴t=![]() ,
,
故答案为:2或![]() .
.





科目:初中数学 来源: 题型:
【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动.投放A,B两种款型的单车共100辆,总价值36800元.试问本次试点投放的A型车与B型车各多少辆?
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有A型车与B型车各多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化,某学校决定举行学生趣味运动会,将比赛项目确定为袋鼠跳、夹球跑、跳大绳、绑腿跑和拔河赛五种,为了解学生对这五项运动的喜欢情况,随机调查了该校a名学生最喜欢的一种项目(每名学生必选且只能选择五项中的一种),并将调查结果绘制成如图不完整的统计图表:
学生最喜欢的活动项目的人数统计表

根据图表中提供的信息,解答下列问题:
(1)a= ,b= ,c= .
(2)请将条形统计图补充完整;
(3)根据调查结果,请你估计该校3000名学生中有多少名学生最喜欢绑腿跑;
(4)根据调查结果,某班决定从这五项(袋鼠跳、夹球跑、跳大绳、绑腿跑和拔河赛可分别记为A、B、C、D、E)中任选其中两项进行训练,用画树状图或列表的方法求恰好选到学生喜欢程度最高的两项的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】佳乐家超市元旦期间搞促销活动,活动方案如下表:
一次性购物 | 优惠方案 |
不超过200元 | 不给予优惠 |
超过200元,而不超过1000元 | 优惠10% |
超过1000元 | 其中1000元按8.5折优惠,超过部分按7折优惠 |
小颖在促销活动期间两次购物分别支付了134元和913元.
(1)小颖两次购买的物品如果不打折,应支付多少钱?
(2)在此活动中,他节省了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
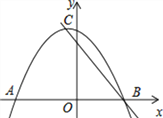
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣2,0)、B(x1,0),且1<x1<2,与y轴正半轴的交点在(0,2)的上方,顶点为C.直线y=kx+m(k≠0)经过点C、B.则下列结论:①b>a;②2a﹣b>﹣1;③2a+c<0;④k>a+b;⑤k<﹣1. 其中正确的结论有_________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知C为线段AB的中点,E为线段AB上的点,点D为线段AE的中点.
(1)若线段AB=a,CE=b,|a﹣15|+(b﹣4.5)2=0,求a,b的值;
(2)如图1,在(1)的条件下,求线段DE的长;
(3)如图2,若AB=15,AD=2BE,求线段CE的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AD=80,点B、点C都是线段AD上的点.
(1)如图1,若点M为AB的中点,点N为BD的中点,求线段MN的长;
(2)如图2,若BC=10,点E是线段AC的中点,点F是线段BD的中点,求EF的长;
(3)如图3,若AB=5,BC=10,点P、Q分别从B、C出发向点D运动,运动速度分别为每秒移动1个单位和每秒移动4个单位,运动时间为t秒,点E为AQ的中点,点F为PD的中点,若PE=QF,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
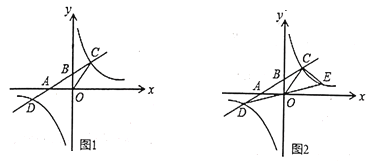
【题目】如图1,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() )两点与x轴,y轴分别交于A、B(0,2)两点,如果
)两点与x轴,y轴分别交于A、B(0,2)两点,如果![]() 的面积为6.
的面积为6.
(1)求点A的坐标;
(2)求一次函数和反比例函数的解析式;
(3)如图2,连接DO并延长交反比例函数的图象于点E,连接CE,求点E的坐标和![]() 的面积
的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
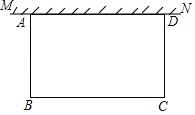
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com