
【题目】如图1,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() )两点与x轴,y轴分别交于A、B(0,2)两点,如果
)两点与x轴,y轴分别交于A、B(0,2)两点,如果![]() 的面积为6.
的面积为6.
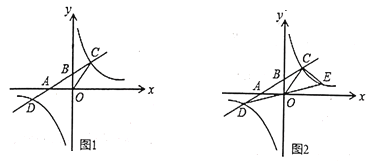
(1)求点A的坐标;
(2)求一次函数和反比例函数的解析式;
(3)如图2,连接DO并延长交反比例函数的图象于点E,连接CE,求点E的坐标和![]() 的面积
的面积
【答案】(1)A(﹣4,0);(2)![]() ,
,![]() ;(3)
;(3)![]() ,8
,8
【解析】
(1)由三角形面积求出OA=4,即可求得A(-4,0).
(2)利用待定系数法即可求出一次函数的解析式,进而求得C点的坐标,把C点的坐标代入![]() ,求出m的值,得到反比例函数的解析式;
,求出m的值,得到反比例函数的解析式;
(3)先联立两函数解析式得出D点坐标,根据中心对称求得E点的坐标,然后根据三角形的面积公式计算△CED的面积即可.
(1)如图1,
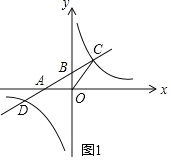
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 的面积为6,
的面积为6,
∴![]() ,
,
∵![]() ,
,
∴OA=4,
∴A(﹣4,0);
(2)如图1,把![]() 代入
代入![]() 得
得![]() ,
,
解得![]() ,
,
∴一次函数的解析式为![]() ,
,
把![]() 代入得,
代入得,![]() ,
,
∴![]() ,
,
∵点C在反比例函数![]() 的图象上,
的图象上,
∴m=2×3=6,
∴反比例函数的解析式为![]() ;
;
(3)如图2,作![]() 轴于F,
轴于F,![]() 轴于H,
轴于H,
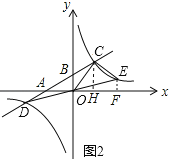
解 ,得
,得![]() ,
,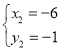 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() =
=![]()


科目:初中数学 来源: 题型:
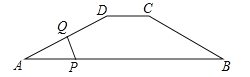
【题目】如图,在四边形ABCD中,DC∥AB,AD=5,CD=3,sinA=sinB=![]() ,动点P自A点出发,沿着边AB向点B匀速运动,同时动点Q自点A出发,沿着边AD﹣DC﹣CB匀速运动,速度均为每秒1个单位,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(秒)时,△APQ的面积为s,则s关于t的函数图象是( )
,动点P自A点出发,沿着边AB向点B匀速运动,同时动点Q自点A出发,沿着边AD﹣DC﹣CB匀速运动,速度均为每秒1个单位,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(秒)时,△APQ的面积为s,则s关于t的函数图象是( )
A. 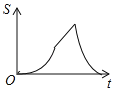 B.
B. 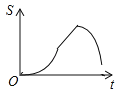
C. 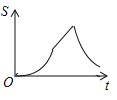 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△AOB的边长为4,点P从点O出发,沿OA以每秒1个单位的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段BP的中点绕点P按顺时针方向旋转60°得点C,点C随点P的运动而运动,连接CP、CA.在点P从O向A运动的过程中,当△PCA为直角三角形时t的值为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强打算找印刷公司设计一款新年贺卡并印刷.如图1是甲印刷公司设计与印刷卡片计价方式的说明(包含设计费与印刷费),乙公司的收费与印刷卡片数量的关系如图2所示.
(1)分别写出甲乙两公司的收费y(元)与印刷数量x之间的关系式.
(2)如果你是小强,你会选择哪家公司?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,安全快捷、平稳舒适的中国高铁,为世界高速铁路商业运营树立了新的标杆.随着中国特色社会主义进入新时代,作为“中国名片”的高速铁路也将踏上自己的新征程,跑出发展新速度,这就意味着今后外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从A地到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:
(1)普通列车的行驶路程为多少千米?
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )

A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+
x+![]() 分别与x轴、y轴交于B,C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+
分别与x轴、y轴交于B,C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+![]() 经过A,B两点,A点坐标为(﹣1,0).
经过A,B两点,A点坐标为(﹣1,0).
(1)求B、C两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com