练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】为了测量被池塘隔开的A，B两点之间的距离，根据实际情况，作出如图所示图形，其中AB⊥BE，EF⊥BE，AF交BE于D，C在BD上.有四位同学分别测量出以下四组数据，根据所测数据不能求出A，B间距离的是（　　）

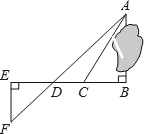
    A. BC，∠ACB B. DE，DC，BC C. EF，DE，BD D. CD，∠ACB，∠ADB

    【答案】B

    【解析】

    根据三角形相似可知，要求出AB，只需求出EF即可．所以借助于相似三角形的性质，根据 即可解答．

    解：此题比较综合，要多方面考虑，

    A、因为知道∠ACB和BC的长，所以可利用∠ACB的正切来求AB的长；

    B、无法求出A，B间距离．

    C、因为△ABD∽△EFD，可利用，求出AB；

    D、可利用∠ACB和∠ADB的正切求出AB；

    据所测数据不能求出A，B间距离的是选项B；

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF=6，AB=4，则AE的长为（　　）

    A. B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知一次函数与反比例函数的图象交于，两点.

    （1）求一次函数与反比例函数的解析式；

    （2） 请根据图象直接写出时的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

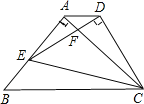
    【题目】 如图，△ABC为等腰直角三角形，∠BAC=90°，BC=1，E为直角边AB上任意一点，以线段CE为斜边作等腰Rt△CDE，连接AD，下列说法：①AC⊥ED；②∠BCE=∠ACD；③△AED∽△ECB；④AD∥BC；⑤四边形ABCD面积的最大值为，其中正确的是______________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明在某次作业中得到如下结果：

    sin27°＋sin283°≈0.122＋0.992＝0.9945，

    sin222°＋sin268°≈0.372＋0.932＝1.0018，

    sin229°＋sin261°≈0.482＋0.872＝0.9873，

    sin237°＋sin253°≈0.602＋0.802＝1.0000，

    sin245°＋sin245°＝＋＝1.

    据此，小明猜想：对于任意锐角α，均有sin2α＋sin2(90°－α)＝1.

    (1)当α＝30°时，验证sin2α＋sin2(90°－α)＝1是否成立；

    (2)小明的猜想是否成立？若成立，请给予证明；若不成立，请举出一个反例．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，线段AB＝1，点P1是线段AB的黄金分割点(且AP1＜BP1，即P1B2＝AP1AB)，点P2是线段AP1的黄金分割点(AP2＜P1P2)，点P3是线段AP2的黄金分割点(AP3＜P2P3)，…，依此类推，则线段AP2017的长度是(　　)

    A. ()2017 B. ()2017 C. ()2017 D. (﹣2)1008

    查看答案和解析>>

    科目：初中数学 来源： 题型：

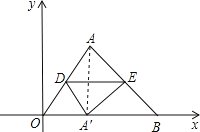
    【题目】在平面直角坐标系中，点O为坐标原点，点A的坐标为（3，4），点B的坐标为（7，0），D，E分别是线段AO，AB上的点，以DE所在直线为对称轴，把△ADE作轴对称变换得△A′DE，点A′恰好在x轴上，若△OA′D与△OAB相似，则OA′的长为________.（结果保留2个有效数字）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

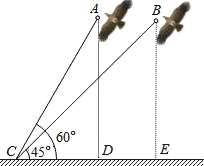
    【题目】在一个阳光明媚，微风习习的周末，小明和小强一起到聂耳文化广场放风筝，放了一会儿，两个人争吵起来：小明说：“我的风筝飞得比你的高”.小强说：“我的风筝引线比你的长，我的风筝飞得更高”.谁的风筝飞得更高呢？于是他们将两个风筝引线的一段都固定在地面上的C处（如图），现已知小明的风筝引线（线段AC）长30米，小强的风筝引线（线段BC）长36米，在C处测得风筝A的仰角为60°，风筝B的仰角为45°，请通过计算说明谁的风筝飞得更高？（结果精确到0.1米，参考数据：≈1.41，≈1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

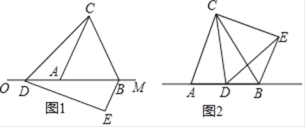
    【题目】已知△ABC是边长为4的等边三角形，边AB在射线OM上，且OA＝6，点D是射线OM上的动点，当点D不与点A重合时，将△ACD绕点C逆时针方向旋转60°得到△BCE，连接DE．

    （1）如图1，求证：△CDE是等边三角形．

    （2）设OD＝t，

    ①当6＜t＜10时，△BDE的周长是否存在最小值？若存在，求出△BDE周长的最小值；若不存在，请说明理由．

    ②求t为何值时，△DEB是直角三角形（直接写出结果即可）．

    查看答案和解析>>

    同步练习册答案