�Ķ����в��ϣ�
����֪��|x|�ļ�������������������x��Ӧ�ĵ���ԭ��ľ��룻��|x|=|x-0|��Ҳ����˵��|x|��ʾ����������x����0��Ӧ��֮��ľ��룻
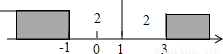
������ۿ����ƹ�Ϊ|x
1-x
2|��ʾ����������x
1��x
2��Ӧ��֮��ľ��룻
�ڽ����У����ǻ᳣�����þ���ֵ�ļ������壺
��1���ⷽ��|x|=2�����ó�������������ԭ�����Ϊ2�ĵ��Ӧ����Ϊ±2�����÷��̵�x=±2��
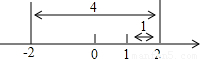
��2���ⲻ��ʽ|x-1|��2����ͼ�����������ҳ�|x-1|=2�Ľ⣬����1�ľ���Ϊ2�ĵ��Ӧ����Ϊ-1��3����|x-1|��2�Ľ�Ϊx��-1��x��3��
��3���ⷽ��|x-1|+|x+2|=5���ɾ���ֵ�ļ�������֪���÷��̱�ʾ������������1��-2�ľ���֮��Ϊ5�ĵ��Ӧ��x��ֵ���������ϣ�1��-2�ľ���Ϊ3�����㷽�̵�x��Ӧ����1���ұ�-2����ߣ���x��Ӧ����1���ұߣ���ͼ���Կ���x=2��ͬ������x��Ӧ����-2����ߣ��ɵ�x=-3����ԭ���̵Ľ���x=2��x=-3��
�ο��Ķ����ϣ�����������⣺
��1������|x+3|=4�Ľ�Ϊ______��
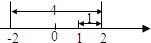
��2���ⲻ��ʽ|x-3|+|x+4|��9��
��3����|x-3|-|x+4|��a�������x����������a��ȡֵ��Χ��

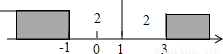

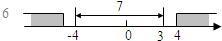
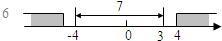



 28��
28��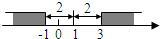 �Ķ����в��ϣ�
�Ķ����в��ϣ�