
【题目】如图,在平面直角坐标系中,线段AB的端点坐标为A(-2,4),B(4,2),直线y=kx-2与线段AB有交点,则K的值不可能是( )
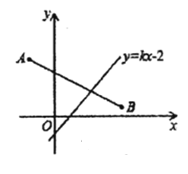
A. -5B. -2C. 3D. 5
【答案】B
【解析】
当直线y=kx-2与线段AB的交点为A点时,把A(-2,4)代入y=kx-2,求出k=-3,根据一次函数的有关性质得到当k≤-3时直线y=kx-2与线段AB有交点;当直线y=kx-2与线段AB的交点为B点时,把B(4,2)代入y=kx-2,求出k=1,根据一次函数的有关性质得到当k≥1时直线y=kx-2与线段AB有交点,从而能得到正确选项.
把A(-2,4)代入y=kx-2得,4=-2k-2,解得k=-3,
∴当直线y=kx-2与线段AB有交点,且过第二、四象限时,k满足的条件为k≤-3;
把B(4,2)代入y=kx-2得,4k-2=2,解得k=1,
∴当直线y=kx-2与线段AB有交点,且过第一、三象限时,k满足的条件为k≥1.
即k≤-3或k≥1.
所以直线y=kx-2与线段AB有交点,则k的值不可能是-2.
故选B.


科目:初中数学 来源: 题型:
【题目】如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)
![]()
(1)数轴上点B对应的数是______.
(2)经过几秒,点M、点N分别到原点O的距离相等?
(3)当点M运动到什么位置时,恰好使AM=2BN?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( ).
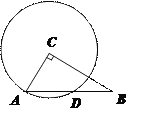
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一定数目的点或大小相同的圆在等距离的排列下可以形成一个等边三角形数阵.古希腊著名数学家毕达哥拉斯用数![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ……这些数量的(石子),都成功的排成了等边三角形数阵..
……这些数量的(石子),都成功的排成了等边三角形数阵..
(问题提出)![]() 结果等于多少?
结果等于多少?
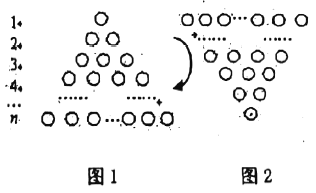
在图1所示的等边三角形数阵中,前![]() 行有
行有![]() 个圆圈,前
个圆圈,前![]() 行有
行有![]() 个圆圈,即
个圆圈,即![]() ,前
,前![]() 行有
行有![]() 个圆圈,即
个圆圈,即![]() ,…,则前
,…,则前![]() 行所有圆圈个数总和为
行所有圆圈个数总和为![]()
将图1旋转至图2,观察这两个三角形数阵中同一行圆圈个数(如第![]() 行的圆圈个数分别为
行的圆圈个数分别为![]() 个,
个,![]() 个),发现同一行圆圈个数之和均为___________个,由此可得两个图前
个),发现同一行圆圈个数之和均为___________个,由此可得两个图前![]() 行圆圈个数总和为:
行圆圈个数总和为:![]() ___________,因此,
___________,因此,![]() ___________.
___________.
(问题延伸)![]() 结果等于多少?
结果等于多少?
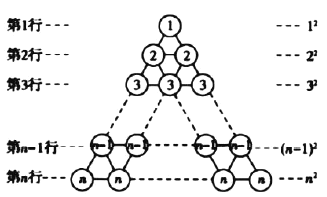
图3
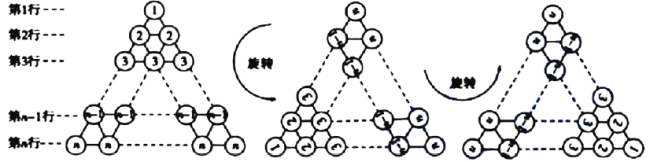
图4
在图3所示的等边三角形数阵中,第![]() 行圆圈中的数为
行圆圈中的数为![]() ,即
,即![]() ,第
,第![]() 行两个圆圈中数字的和为
行两个圆圈中数字的和为![]() .即
.即![]() …,第
…,第![]() 行
行![]() 个圆圈中数字的和为
个圆圈中数字的和为![]() (共
(共![]() 个).即
个).即![]() .这样,该三角形数阵中所有圆圈中数字的和为
.这样,该三角形数阵中所有圆圈中数字的和为![]() .
.
将该三角形数阵经两次旋转可得如图4所示的三个三角形数阵,观察这三个三角形数阵中各行同一位置上圆圈中的数字(如第![]() 行的第一个圆圈中的数字分别为
行的第一个圆圈中的数字分别为![]() ,
,![]() ,
,![]() ),发现相同位置上三个圆圈中数字之和均为___________,由此可得,这三个三角形数阵所有圆圈中数字的总和为:
),发现相同位置上三个圆圈中数字之和均为___________,由此可得,这三个三角形数阵所有圆圈中数字的总和为:![]() ___________,因此,
___________,因此,![]() ___________.
___________.
(规律应用)
根据以上发现,计算:![]() 的结果为___________.
的结果为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在数轴上标出数﹣4.5,﹣2,1,3.5所对应的点A,B,C,D;
(2)C,D两点间距离=_____;B,C两点间距离=_____;
(3)数轴上有两点M,N,点M对应的数为a,点N对应的数为b,那么M,N两点之间的距离=_____;
(4)若动点P,Q分别从点B,C同时出发,沿数轴负方向运动;已知点P的速度是每秒1个单位长度,点Q的速度是每秒2个单位长度,问①t为何值时P,Q两点重合?②t为何值时P,Q两点之间的距离为1?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数![]() 的图象如图所示,以下结论:
的图象如图所示,以下结论:
①常数m<﹣1;
②在每个象限内,y随x的增大而增大;
③若A(﹣1,h),B(2,k)在图象上,则h<k;
④若P(x,y)在图象上,则P′(﹣x,﹣y)也在图象上.
其中正确的是( )
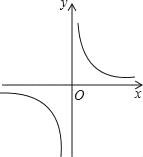
A. ①② B. ②③ C. ③④ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB中,OA=OB=10cm,∠AOB=80°,以点O为圆心,半径为6cm的优弧弧MN分别交OA,OB于点M,N.
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得OP′.求证:AP=BP′;
(2)点T在左半弧上,若AT与弧相切,求AT的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的海岸线l上有AB两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.(结果都保留根号)
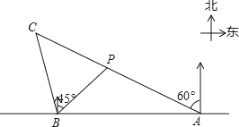
(1)求点P到海岸线l的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
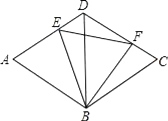
【题目】如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com