
【题目】用一定数目的点或大小相同的圆在等距离的排列下可以形成一个等边三角形数阵.古希腊著名数学家毕达哥拉斯用数![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ……这些数量的(石子),都成功的排成了等边三角形数阵..
……这些数量的(石子),都成功的排成了等边三角形数阵..
(问题提出)![]() 结果等于多少?
结果等于多少?
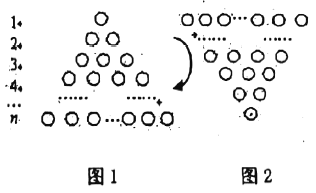
在图1所示的等边三角形数阵中,前![]() 行有
行有![]() 个圆圈,前
个圆圈,前![]() 行有
行有![]() 个圆圈,即
个圆圈,即![]() ,前
,前![]() 行有
行有![]() 个圆圈,即
个圆圈,即![]() ,…,则前
,…,则前![]() 行所有圆圈个数总和为
行所有圆圈个数总和为![]()
将图1旋转至图2,观察这两个三角形数阵中同一行圆圈个数(如第![]() 行的圆圈个数分别为
行的圆圈个数分别为![]() 个,
个,![]() 个),发现同一行圆圈个数之和均为___________个,由此可得两个图前
个),发现同一行圆圈个数之和均为___________个,由此可得两个图前![]() 行圆圈个数总和为:
行圆圈个数总和为:![]() ___________,因此,
___________,因此,![]() ___________.
___________.
(问题延伸)![]() 结果等于多少?
结果等于多少?
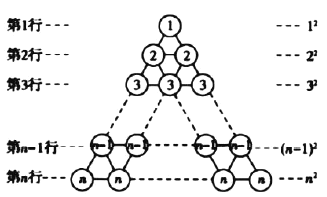
图3
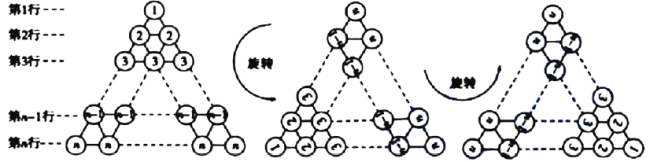
图4
在图3所示的等边三角形数阵中,第![]() 行圆圈中的数为
行圆圈中的数为![]() ,即
,即![]() ,第
,第![]() 行两个圆圈中数字的和为
行两个圆圈中数字的和为![]() .即
.即![]() …,第
…,第![]() 行
行![]() 个圆圈中数字的和为
个圆圈中数字的和为![]() (共
(共![]() 个).即
个).即![]() .这样,该三角形数阵中所有圆圈中数字的和为
.这样,该三角形数阵中所有圆圈中数字的和为![]() .
.
将该三角形数阵经两次旋转可得如图4所示的三个三角形数阵,观察这三个三角形数阵中各行同一位置上圆圈中的数字(如第![]() 行的第一个圆圈中的数字分别为
行的第一个圆圈中的数字分别为![]() ,
,![]() ,
,![]() ),发现相同位置上三个圆圈中数字之和均为___________,由此可得,这三个三角形数阵所有圆圈中数字的总和为:
),发现相同位置上三个圆圈中数字之和均为___________,由此可得,这三个三角形数阵所有圆圈中数字的总和为:![]() ___________,因此,
___________,因此,![]() ___________.
___________.
(规律应用)
根据以上发现,计算:![]() 的结果为___________.
的结果为___________.
【答案】(问题提出)n+1;n(n+1);![]() ;(问题延伸)2n+1;
;(问题延伸)2n+1; ![]() ×(2n+1);
×(2n+1);![]() (规律应用)1345.
(规律应用)1345.
【解析】
(问题提出)根据图形可发现同一行圆圈个数之和均为(n+1)个,由此可得两个图前![]() 行圆圈个数总和为:
行圆圈个数总和为:![]() n(n+1),因此可求出
n(n+1),因此可求出![]() ;
;
(问题延伸)根据材料可得相同位置上三个圆圈中数字之和为![]() +
+![]() +
+![]() =2n+1,由此可得,这三个三角形数阵所有圆圈中数字的总和为:
=2n+1,由此可得,这三个三角形数阵所有圆圈中数字的总和为:![]()
![]() ×(2n+1),因此变形即可求出
×(2n+1),因此变形即可求出![]() ;
;
(规律应用)根据规律即可化简求解.
(问题提出)观察这两个三角形数阵中同一行圆圈个数(如第![]() 行的圆圈个数分别为
行的圆圈个数分别为![]() 个,
个,![]() 个),发现同一行圆圈个数之和均为(n+1)个,由此可得两个图前
个),发现同一行圆圈个数之和均为(n+1)个,由此可得两个图前![]() 行圆圈个数总和为:
行圆圈个数总和为:![]() n(n+1),因此,
n(n+1),因此,![]()
![]() ,
,
故答案为:n+1;n(n+1);![]() ;
;
(问题延伸)
∵![]() +
+![]() +
+![]() =2n+1,
=2n+1,
∴相同位置上三个圆圈中数字之和为![]() +
+![]() +
+![]() =2n+1,
=2n+1,
∴这三个三角形数阵所有圆圈中数字的总和为:![]()
![]() ×(2n+1),
×(2n+1),
∴![]() =
=![]()
故答案为:2n+1; ![]() ×(2n+1);
×(2n+1);![]()
(规律应用)![]()
=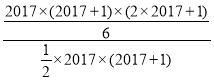
=![]()
=1345
故答案为:1345.


科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于A、B两点,点P在函数
轴交于A、B两点,点P在函数![]() 的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).
的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).
A. 2个 B. 3个 C. 4个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
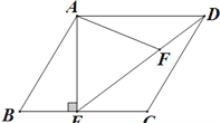
(1)求证:∠DAF=∠CDE;
(2)求证:△ADF∽△DEC;
(3)若AE=6,AD=8,AB=7,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学举行了百科知识竞赛,为了解此次竞赛成绩的情况,随机抽取部分参赛学生的成绩,整理并制作出如下不完整的统计表和统计图,请根据图表信息解答以下问题:
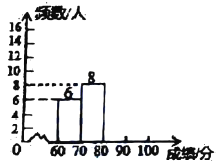

组别 | 成绩 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
(1)表中![]() ___________.
___________.
(2)补全频数分布直方图
(3)计算扇形统计图中“![]() ”对应的圆心角度数.
”对应的圆心角度数.
(4)该大学共有![]() 人参加竞赛,若成绩在
人参加竞赛,若成绩在![]() 分以上(包括
分以上(包括![]() 分)的为“优”等,根据抽样结果,估计该校参赛学生成绩达到“优”等的人数.
分)的为“优”等,根据抽样结果,估计该校参赛学生成绩达到“优”等的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家想要从某场购买洗衣机和烘干机各一台,现在分别从![]() 两个品牌中各选中一款洗衣机和一款烘干机,它们的单价如表1所示.目前该商场有促销活动,促销方案如表2所示.
两个品牌中各选中一款洗衣机和一款烘干机,它们的单价如表1所示.目前该商场有促销活动,促销方案如表2所示.
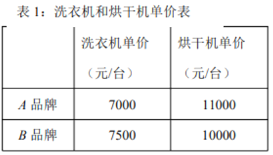
表2:商场促销方案
1. 所有商品均享受8折优惠.
2. 所有洗衣机均可享受节能减排补
贴,补贴标准为:在折后价的基础t.
再减免13%。
3.若同时购买同品牌洗 衣机和烘干
机,额外可享受“满两件减400元"
则选择_____品种的洗衣机和_____品种的烘干机支付总费用最低,支付总费用最低为___________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,线段AB的端点坐标为A(-2,4),B(4,2),直线y=kx-2与线段AB有交点,则K的值不可能是( )
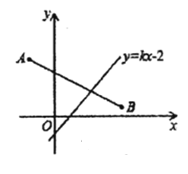
A. -5B. -2C. 3D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围;
(2)若k取小于1的整数,且此方程的解为整数,则求出此方程的两个整数根;
(3)在(2)的条件下,二次函数![]() 与x轴交于A、B两点(A点在B点的左侧),D点在此抛物线的对称轴上,若∠DAB=60,直接写出D点的坐标.
与x轴交于A、B两点(A点在B点的左侧),D点在此抛物线的对称轴上,若∠DAB=60,直接写出D点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店分两次购进![]() 、
、![]() 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:

(1)求![]() 、
、![]() 两种商品每件的进价分别是多少元?
两种商品每件的进价分别是多少元?
(2)商场决定![]() 商品以每件
商品以每件![]() 元出售,
元出售,![]() 商品以每件
商品以每件![]() 元出售.为满足市场需求,需购进
元出售.为满足市场需求,需购进![]() 、
、![]() 两种商品共
两种商品共![]() 件,且
件,且![]() 商品的数量不少于
商品的数量不少于![]() 种商品数量的
种商品数量的![]() 倍,请你求出获利最大的进货方案,并确定最大利润.
倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com