
【题目】小明家想要从某场购买洗衣机和烘干机各一台,现在分别从![]() 两个品牌中各选中一款洗衣机和一款烘干机,它们的单价如表1所示.目前该商场有促销活动,促销方案如表2所示.
两个品牌中各选中一款洗衣机和一款烘干机,它们的单价如表1所示.目前该商场有促销活动,促销方案如表2所示.
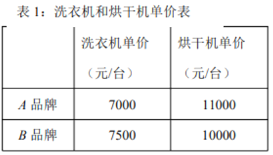
表2:商场促销方案
1. 所有商品均享受8折优惠.
2. 所有洗衣机均可享受节能减排补
贴,补贴标准为:在折后价的基础t.
再减免13%。
3.若同时购买同品牌洗 衣机和烘干
机,额外可享受“满两件减400元"
则选择_____品种的洗衣机和_____品种的烘干机支付总费用最低,支付总费用最低为___________元.
【答案】B B 12820
【解析】
根据题意分四种方案:A品牌洗衣机和A品牌烘干机;A品牌洗衣机和B品牌烘干机;B品牌洗衣机和A品牌烘干机;B品牌洗衣机和B品牌烘干机,分别计算出支付总费用即可得出答案
解:购买A品牌洗衣机和A品牌烘干机费用=(7000+11000)![]() 7000
7000![]() =13272(元)
=13272(元)
购买A品牌洗衣机和B品牌烘干机费用=![]() 7000
7000![]() =12872(元)
=12872(元)
购买B品牌洗衣机和A品牌烘干机费用=![]() 7500
7500![]() =14020(元)
=14020(元)
购买B品牌洗衣机和B品牌烘干机费用=(7500+10000)![]() 7500
7500![]() =12820(元)
=12820(元)
综上所述,选择B品种的洗衣机和B品种的烘干机支付总费用最低,支付总费用最低为12820元.
故答案为:B,B,12820


科目:初中数学 来源: 题型:
【题目】蜗牛从某点O开始沿东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬行的各段路程依次为(单位:厘米):![]() .问:
.问:
(1)蜗牛最后是否回到出发点O?
(2)蜗牛离开出发点O最远是多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,则蜗牛可得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,正方形OABC的顶点A和C分别在x轴和y轴正半轴上,点B坐标为(3,3),抛物线y=﹣x2+bx+c过点A、C,交x轴负半轴于点D,与BC边的另一个交点为E,抛物线的顶点为M,对称轴交x轴于点N.
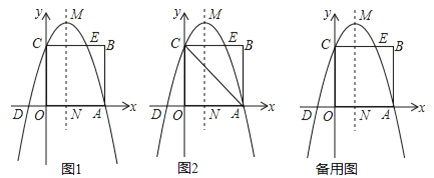
(1)求抛物线的函数关系式;
(2)点P在直线MN上,求当PE+PA的值最小时点P的坐标;
(3)如图2,探索在x轴是否存在一点F,使∠CFO=∠CDO﹣∠CAO?若存在,求点F的坐标;不存在,说明理由;
(4)将抛物线沿y轴方向平移m个单位后,顶点为Q,若QO平分∠CQN,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,△ABC的三个顶点坐标分别为A(-4,1)、B(-1,1)、C(-4,3).
(1)画出Rt△ABC关于原点O成中心对称的图形Rt△A1B1C1;
(2)若Rt△ABC与Rt△A2BC2关于点B中心对称,则点A2的坐标为 、C2的坐标为 .
(3)求点A绕点B旋转180°到点A2时,点A在运动过程中经过的路程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一定数目的点或大小相同的圆在等距离的排列下可以形成一个等边三角形数阵.古希腊著名数学家毕达哥拉斯用数![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ……这些数量的(石子),都成功的排成了等边三角形数阵..
……这些数量的(石子),都成功的排成了等边三角形数阵..
(问题提出)![]() 结果等于多少?
结果等于多少?
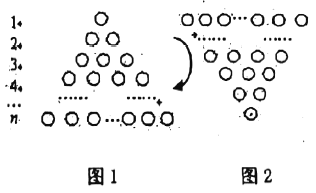
在图1所示的等边三角形数阵中,前![]() 行有
行有![]() 个圆圈,前
个圆圈,前![]() 行有
行有![]() 个圆圈,即
个圆圈,即![]() ,前
,前![]() 行有
行有![]() 个圆圈,即
个圆圈,即![]() ,…,则前
,…,则前![]() 行所有圆圈个数总和为
行所有圆圈个数总和为![]()
将图1旋转至图2,观察这两个三角形数阵中同一行圆圈个数(如第![]() 行的圆圈个数分别为
行的圆圈个数分别为![]() 个,
个,![]() 个),发现同一行圆圈个数之和均为___________个,由此可得两个图前
个),发现同一行圆圈个数之和均为___________个,由此可得两个图前![]() 行圆圈个数总和为:
行圆圈个数总和为:![]() ___________,因此,
___________,因此,![]() ___________.
___________.
(问题延伸)![]() 结果等于多少?
结果等于多少?
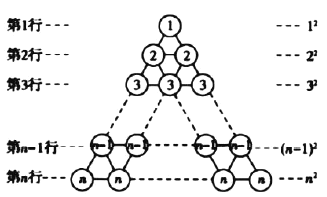
图3
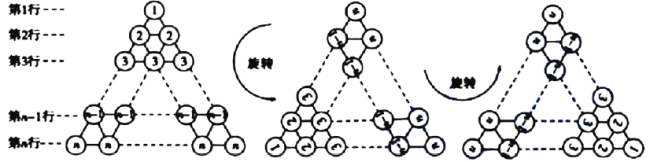
图4
在图3所示的等边三角形数阵中,第![]() 行圆圈中的数为
行圆圈中的数为![]() ,即
,即![]() ,第
,第![]() 行两个圆圈中数字的和为
行两个圆圈中数字的和为![]() .即
.即![]() …,第
…,第![]() 行
行![]() 个圆圈中数字的和为
个圆圈中数字的和为![]() (共
(共![]() 个).即
个).即![]() .这样,该三角形数阵中所有圆圈中数字的和为
.这样,该三角形数阵中所有圆圈中数字的和为![]() .
.
将该三角形数阵经两次旋转可得如图4所示的三个三角形数阵,观察这三个三角形数阵中各行同一位置上圆圈中的数字(如第![]() 行的第一个圆圈中的数字分别为
行的第一个圆圈中的数字分别为![]() ,
,![]() ,
,![]() ),发现相同位置上三个圆圈中数字之和均为___________,由此可得,这三个三角形数阵所有圆圈中数字的总和为:
),发现相同位置上三个圆圈中数字之和均为___________,由此可得,这三个三角形数阵所有圆圈中数字的总和为:![]() ___________,因此,
___________,因此,![]() ___________.
___________.
(规律应用)
根据以上发现,计算:![]() 的结果为___________.
的结果为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点A、点B在数轴上,点C表示-│-3.5│,点D表示-(-2),点E表示-2![]() .
.
![]()
(1)点A表示_______,点B表示_______;
(2)在数轴上表示出点C,点D,点E;
(3)比较大小:_______<_______<_______<_______<_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
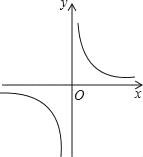
【题目】反比例函数![]() 的图象如图所示,以下结论:
的图象如图所示,以下结论:
①常数m<﹣1;
②在每个象限内,y随x的增大而增大;
③若A(﹣1,h),B(2,k)在图象上,则h<k;
④若P(x,y)在图象上,则P′(﹣x,﹣y)也在图象上.
其中正确的是( )
A. ①② B. ②③ C. ③④ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级全体学生在5名教师的带领下去公园秋游,公园的门票为每人30元.现有两种优惠方案,甲方案:带队老师免费,学生按8折收费;乙方案:师生都按7.5折收费.
(1)若有n名学生,用含n的代数式表示两种优惠方案各需多少元?
(2)当n=70时,采用哪种方案更优惠?
(3)当n=100时,采用哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题(直接写出答案)
(1)2+(﹣2)= ;
(2)1﹣3= ;
(3)(﹣1)×(﹣3)= ;
(4)12÷(﹣3)= ;
(5)﹣32×![]() = ;
= ;
(6)(﹣4)2018×(﹣0.25)2019= ;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com