
【题目】如图1,在平面直角坐标系中,正方形OABC的顶点A和C分别在x轴和y轴正半轴上,点B坐标为(3,3),抛物线y=﹣x2+bx+c过点A、C,交x轴负半轴于点D,与BC边的另一个交点为E,抛物线的顶点为M,对称轴交x轴于点N.
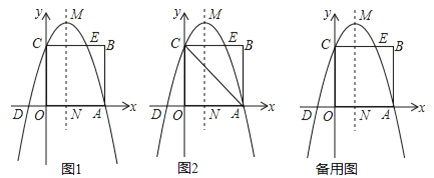
(1)求抛物线的函数关系式;
(2)点P在直线MN上,求当PE+PA的值最小时点P的坐标;
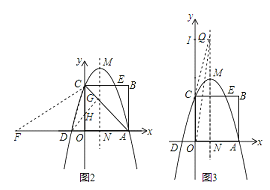
(3)如图2,探索在x轴是否存在一点F,使∠CFO=∠CDO﹣∠CAO?若存在,求点F的坐标;不存在,说明理由;
(4)将抛物线沿y轴方向平移m个单位后,顶点为Q,若QO平分∠CQN,求点Q的坐标.
【答案】(1)y=-x2+2x+3;(2)P(1,2)(3)F(6,0),(-6,0);(4)Q(1, ![]() ),(1,
),(1, ![]() )
)
【解析】试题分析:(1)由已知条件易得点A和点C的坐标,再利用待定系数法即可求得函数的解析式;(2)AC与对称轴的交点就是P,利用待定系数法求得AC的解析式,即可求得点P的坐标;(3)在y轴的正半轴上截取OH=OD=1,则H的坐标是(0,1),延长DH交AC于点G,则DG⊥AC,∠CDH=∠CDO﹣∠CAO,当F在x轴的负半轴上时,当∠CFO=∠CDH=∠CDO﹣∠CAO时,则△CFO∽△CDG,根据相似三角形的对应边的比相等即可求得OF的长,则F的坐标即可求得,然后根据对称性求得F在x轴的正半轴时的坐标;
(4)当抛物线沿y轴的正半轴移动时,Q的横坐标是1,QO平分∠CQN,则CQ=OC,利用勾股定理即可求得Q的纵坐标;同理求得抛物线沿y轴的负半轴移动时Q的坐标.
试题解析: 解:(1)∵四边形OABC是正方形,B的坐标是(3,3),
∴A的坐标是(3,0),C的坐标是(0,3).
根据题意得![]() ,
,
解得:![]() ,
,
则二次函数的解析式是y=﹣x2+2x+3;
(2)设直线AC的解析式是y=ax+b,
![]() ,
,
解得:![]() ,
,
则直线AC的解析式是y=﹣x+3,
当x=1时,y=﹣1+3=2,
则P的坐标是(1,2);
(3)在y=﹣x2+2x+3中令y=0,则﹣x2+2x+3=0,解得x=﹣1或x=3.
则D的坐标是(﹣1,0)A的坐标是(3,0).
在y轴的正半轴上截取OH=OD=1,则H的坐标是(0,1),延长DH交AC于点G,则DG⊥AC;
∵直角△ODF中,OH=OD,
∴∠HDO=45°,
同理,∠CAO=45°,
∴∠HDO=∠CAO.则∠CDH=∠CDO﹣∠CAO.
当F在x轴的负半轴上时,
设DG的解析式是y=ex+f,则![]() ,
,
解得![]() ,则DG的解析式是y=x+1.
,则DG的解析式是y=x+1.
根据题意得:![]() ,
,
解得:![]() ,
,
则G的坐标是(1,2).
则DG=![]() ,CD=
,CD=![]() ,CG=
,CG=![]() .
.
当∠CFO=∠CDH=∠CDO﹣∠CAO时,△CFO∽△CDG,
则![]() ,即
,即![]() ,解得:OF=6,
,解得:OF=6,
则F的坐标是(﹣6,0).
根据对称性可得当F在x轴的正半轴上时F的坐标是(6,0);
(4)当抛物线沿y轴的正半轴移动时,如图3,
设Q的坐标是(1,n).作QI⊥y轴于点I.则IQ=1,IC=n﹣3,
则QO平分∠CQN,则CQ=OC=3,12+(n﹣3)2=32,
解得:n=3+2![]() ,
,
则Q的坐标是(1,3+2![]() );
);
同理,当抛物线沿y轴的负方向移动时Q的坐标是(1,3﹣2![]() ).
).
总之,Q的坐标是(1,3+2![]() )或(1,3﹣2
)或(1,3﹣2![]() ).
).


科目:初中数学 来源: 题型:
【题目】(1)5(a2b-ab2)-2(ab2+3a2b);
(2)-2a+(3a-1)-(a-5);
(3)先化简,再求值:![]() x-2(x-
x-2(x-![]() y2)+(
y2)+(![]() x+
x+![]() y2),其中x=-2,y=
y2),其中x=-2,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举办中学生足球赛,初中男子组共有市直学校的A、B两队和县区学校的e、f、g、h四队报名参赛,六支球队分成甲、乙两组,甲组由A、e、f三队组成,乙组由B、g、h三队组成,现要从甲、乙两组中各随机抽取一支球队进行首场比赛.
(1)在甲组中,首场比赛抽到e队的概率是 ;
(2)请你用画树状图或列表的方法,求首场比赛出场的两个队都是县区学校队的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标平面内,小明站在点A(﹣10,0)处观察y轴,眼睛距地面1.5米,他的前方5米处有一堵墙DC,若墙高DC=2米,则小明在y轴上的盲区(即OE的长度)为_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
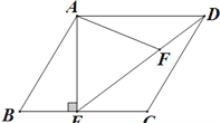
(1)求证:∠DAF=∠CDE;
(2)求证:△ADF∽△DEC;
(3)若AE=6,AD=8,AB=7,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学会生随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家想要从某场购买洗衣机和烘干机各一台,现在分别从![]() 两个品牌中各选中一款洗衣机和一款烘干机,它们的单价如表1所示.目前该商场有促销活动,促销方案如表2所示.
两个品牌中各选中一款洗衣机和一款烘干机,它们的单价如表1所示.目前该商场有促销活动,促销方案如表2所示.
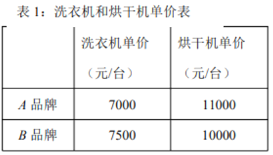
表2:商场促销方案
1. 所有商品均享受8折优惠.
2. 所有洗衣机均可享受节能减排补
贴,补贴标准为:在折后价的基础t.
再减免13%。
3.若同时购买同品牌洗 衣机和烘干
机,额外可享受“满两件减400元"
则选择_____品种的洗衣机和_____品种的烘干机支付总费用最低,支付总费用最低为___________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DBC成立的是 ( )

A. AB=CD B. AC=BD C. ∠A=∠D D. ∠ABC=∠DCB
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com