
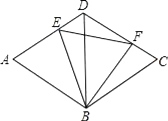
【题目】如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由.
【答案】(1)证明见解析(2)等边三角形
【解析】试题分析:(1)由菱形ABCD的边长为2,BD=2,易得BD=BC,∠C=∠BDE=60°,又由AE+CF=2,易得DE=CF,则可证得:△BDE≌△BCF;
(2)由△BDE≌△BCF,易得BE=BF,∠EBF=60°,则可证得△BEF是等边三角形.
试题解析:(1)证明:∵菱形ABCD的边长为2,BD=2,∴BC=BD=CD=AD=2,∴∠C=∠CDB=60°.∵∠BDE=∠BDC,∴∠BDE=∠C.∵AE+DE=AD=2,AE+CF=2,∴DE=CF.在△BDE和△BCF中,∵BD=BC,∠BDE=∠C,DE=CF,∴△BDE≌△BCF(SAS);
(2)解:等边三角形.理由如下:
∵△BDE≌△BCF,∴BE=BF,∠CBF=∠DBE.∵∠CBF+∠DBF=60°,∴∠EBF=∠EBD+∠DBF=∠CBF+∠DBF=60°,∴△BEF是等边三角形.


 能力评价系列答案
能力评价系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,线段AB的端点坐标为A(-2,4),B(4,2),直线y=kx-2与线段AB有交点,则K的值不可能是( )
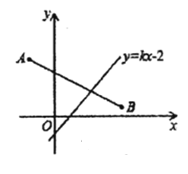
A. -5B. -2C. 3D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线l:y=ax2+bx+c(a,b,c均不为0)的顶点为M,与y轴的交点为N,我们称以N为顶点,对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线,直线MN为抛物线l的衍生直线.
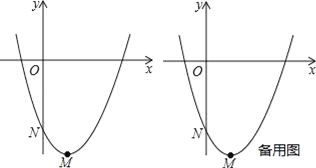
(1)如图,抛物线y=x2﹣2x﹣3的衍生抛物线的解析式是 ,衍生直线的解析式是 ;
(2)若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1,求这条抛物线的解析式;
(3)如图,设(1)中的抛物线y=x2﹣2x﹣3的顶点为M,与y轴交点为N,将它的衍生直线MN先绕点N旋转到与x轴平行,再沿y轴向上平移1个单位得直线n,P是直线n上的动点,是否存在点P,使△POM为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店分两次购进![]() 、
、![]() 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:

(1)求![]() 、
、![]() 两种商品每件的进价分别是多少元?
两种商品每件的进价分别是多少元?
(2)商场决定![]() 商品以每件
商品以每件![]() 元出售,
元出售,![]() 商品以每件
商品以每件![]() 元出售.为满足市场需求,需购进
元出售.为满足市场需求,需购进![]() 、
、![]() 两种商品共
两种商品共![]() 件,且
件,且![]() 商品的数量不少于
商品的数量不少于![]() 种商品数量的
种商品数量的![]() 倍,请你求出获利最大的进货方案,并确定最大利润.
倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017山东德州第21题)如图所示,某公路检测中心在一事故多发地带安装了一个测速仪,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用的时间为0.9秒.已知∠B=30°,∠C=45°
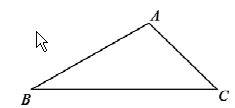
(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80km/h,那么这辆汽车是否超速?请说明理由.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】潮州市某学校为了改善办学条件,购置一批电子白板和台式电脑合共24台.经招投标,一台电子白板每台9000元,一台台式电脑每台3000元,设学校购买电子白板和台式电脑总费用为![]() 元,购买了
元,购买了![]() 台电子白板,并且台式电脑的台数不超过电子白板台数的3倍.
台电子白板,并且台式电脑的台数不超过电子白板台数的3倍.
(1)请求出![]() 与
与![]() 的函数解析式,并直接写出
的函数解析式,并直接写出![]() 的取值范围
的取值范围
(2)请问当购买多少台电子白板时,学校购置电子白板和台式电脑的总费用最少,最少多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.

(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线MN表示一条铁路,A,B是两个城市,它们到铁路的垂直距离分别为AA1=20km,BB1=40km,已知A1B1=80km,现要在A1,B1之间设一个中转站P,使两个城市到中转站的距离之和最短,请你设计一种方案确定P点的位置,并求这个最短距离.
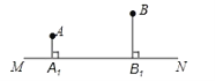
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:
“宇番2号”番茄挂果数量统计表
挂果数量x(个) | 频数(株) | 频率 |
25≤x<35 | 6 | 0.1 |
35≤x<45 | 12 | 0.2 |
45≤x<55 | a | 0.25 |
55≤x<65 | 18 | b |
65≤x<75 | 9 | 0.15 |
请结合图表中的信息解答下列问题:
(1)统计表中,a= ,b= ;
(2)将频数分布直方图补充完整;
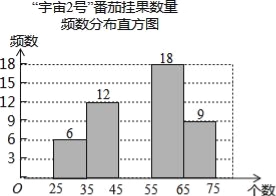
(3)若绘制“番茄挂果数量扇形统计图”,则挂果数量在“35≤x<45”所对应扇形的圆心角度数为 °;
(4)若所种植的“宇番2号”番茄有1000株,则可以估计挂果数量在“55≤x<65”范围的番茄有 株.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com